题目内容
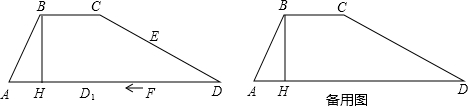
如图，在梯形纸片ABCD中，BC∥AD，∠A+∠D=90°，tanA=2，过点B作BH⊥AD于H，BC=BH=2．动点F从点D出发，以每秒1个单位的速度沿DH运动到点H停止，在运动过程中，过点F作FE⊥AD交折线D-C-B于点E，将纸片沿直线EF折叠，点C、D的对应点分别是点C1、D1．设F点运动的时间是x秒（x＞0）．
（1）当点E和点C重合时，求运动时间x的值；
（2）在整个运动过程中，设△EFD1或四边形EFD1C1与梯形ABCD重叠部分面积为S，请直接写出S与x之间的函数关系式和相应自变量x的取值范围；
（3）平移线段CD，交线段BH于点G，交线段AD于点P．在直线BC上存在点I，使△PGI为等腰直角三角形．请求出线段IB的所有可能的长度．
（1）当点E和点C重合时，求运动时间x的值；
（2）在整个运动过程中，设△EFD1或四边形EFD1C1与梯形ABCD重叠部分面积为S，请直接写出S与x之间的函数关系式和相应自变量x的取值范围；
（3）平移线段CD，交线段BH于点G，交线段AD于点P．在直线BC上存在点I，使△PGI为等腰直角三角形．请求出线段IB的所有可能的长度．
分析：（1）过C作GC∥AB交AD于G，通过勾股定理就可以求出AH=1，AB=
，再得出四边形ABCG是平行四边求出DH，过C作CM⊥AD交AD于M，求出DM的值即可；
（2）分四种情况讨论，如图4，当0＜x≤3.5时，如图5，3.5＜x≤4时，作GM⊥AD于M，如图6，当4＜x≤5时，作GM⊥AD于M，当5＜x≤6时，可以分别求出S与x之间的环数关系式；
（3）分三种情况：当点P为直角顶点时，当点I为直角顶点时，当点G为直角顶点时，利用全等三角形的性质就可以求出结论．
| 5 |
（2）分四种情况讨论，如图4，当0＜x≤3.5时，如图5，3.5＜x≤4时，作GM⊥AD于M，如图6，当4＜x≤5时，作GM⊥AD于M，当5＜x≤6时，可以分别求出S与x之间的环数关系式；
（3）分三种情况：当点P为直角顶点时，当点I为直角顶点时，当点G为直角顶点时，利用全等三角形的性质就可以求出结论．
解答：解：（1）过C作GC∥AB交AD于G，
∴∠CGD=∠A，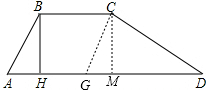
∵∠A+∠D=90°，
∴∠CGD+∠D=90°，
∴∠DCG=90°．
在Rt△AHB中，tanA=2，BH=2，
∴AH=1，AB=
，
∵BC∥AD，CG∥AB，
∴四边形ABCG是平行四边形，
∴AG=BC=2，CG=AB=
，
∴CD=2
，GD=5，
∴DH=6．
过C作CM⊥AD交AD于M，
∴DM=4，当点E和点C重合时x=4．
（2）如图4，当0＜x≤3.5时，
S=
D1F•EF=
x•
x=
x2；
如图5，3.5＜x≤4时，作GM⊥AD于M，
S=
D1F•EF-
D1A•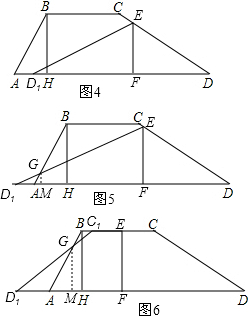
GM．
D1A=2x-7
设GM=a，则AM=
a，
∵
=
a，
∴
=
，
∴a=
，
即GM=
．
∴S=
x2-
（2x-7）×
；
=-
x2+
x-
；
如图6，当4＜x≤5时，作GM⊥AD于M，
S=
（C1E+D1F）×2-
D1A•GM
=
（x-4+x）×2-
（2x-7）×
=-
x2+
x-
；
当5＜x≤6时，
S=
（BE+AF）•EF
=
（6-x+7-x）×2
=13-2x．
（3）①如图1
当点P为直角顶点时，作IO⊥AD于O，
∴∠POI=90°．∠GPI=90°．
∴∠GPH+∠IPO=90°，∠IPO+∠PIO=90°，
∴∠GPH=∠PIO．
∵△PGI是等腰直角三角形，
∴GP=IP．
∵BH⊥AD，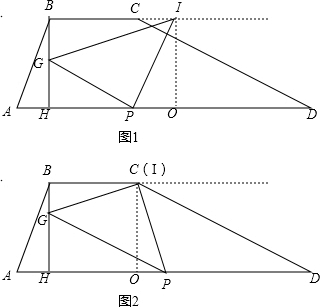
∴∠BHP=90°，
∴∠BHP=∠POI．
在△GHP和△POI中，
，
∴△GHP≌△POI，
∴HP=OI，GH=PO．
∵GP∥CD，
∴∠GPH=∠D．
∵∠A+∠D=90°，
∴∠A+∠GPH=90°，
∵∠A+∠ABH=90°，
∴∠ABH=∠GPH．
∵tanA=2，
∴tan∠ABH=tan∠GPH=
，
∴GH=
HP=
IO=1，
∴IB=2+1=3；
②如图2，当点I为直角顶点时，作IO⊥AD于O，
同理可以得出：△BGI≌△OPI，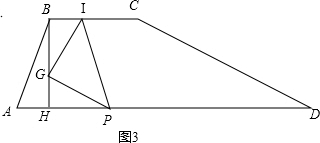
∴IP=IO．
∵IO=BH=2，
∴IB=2；
③如图3，当点G为直角顶点时，
同理可以得出：△BGI≌△HPG，
∴BI=GH，GB=HP．
∵GH=
HP，
∴GH=
BG，
∴GH=
BH=
，
∴BI=
．
综上所述，IB的长度是3，2，
．
∴∠CGD=∠A，
∵∠A+∠D=90°，
∴∠CGD+∠D=90°，
∴∠DCG=90°．
在Rt△AHB中，tanA=2，BH=2，
∴AH=1，AB=
| 5 |
∵BC∥AD，CG∥AB，
∴四边形ABCG是平行四边形，
∴AG=BC=2，CG=AB=
| 5 |
∴CD=2
| 5 |
∴DH=6．
过C作CM⊥AD交AD于M，
∴DM=4，当点E和点C重合时x=4．
（2）如图4，当0＜x≤3.5时，
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
如图5，3.5＜x≤4时，作GM⊥AD于M，
S=
| 1 |
| 2 |
| 1 |
| 2 |
GM．D1A=2x-7
设GM=a，则AM=
| 1 |
| 2 |
∵
| GM |
| D1M |
| 1 |
| 2 |
∴
| a | ||
2x-7+
|
| 1 |
| 2 |
∴a=
| 4x-14 |
| 3 |
即GM=
| 4x-14 |
| 3 |
∴S=
| 1 |
| 4 |
| 1 |
| 2 |
| 4x-14 |
| 3 |
=-
| 13 |
| 12 |
| 28 |
| 3 |
| 49 |
| 3 |
如图6，当4＜x≤5时，作GM⊥AD于M，
S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 4x-14 |
| 3 |
| 4 |
| 3 |
| 34 |
| 3 |
| 61 |
| 3 |
当5＜x≤6时，
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
=13-2x．
（3）①如图1
当点P为直角顶点时，作IO⊥AD于O，
∴∠POI=90°．∠GPI=90°．
∴∠GPH+∠IPO=90°，∠IPO+∠PIO=90°，
∴∠GPH=∠PIO．
∵△PGI是等腰直角三角形，
∴GP=IP．
∵BH⊥AD，
∴∠BHP=90°，
∴∠BHP=∠POI．
在△GHP和△POI中，
|
∴△GHP≌△POI，
∴HP=OI，GH=PO．
∵GP∥CD，
∴∠GPH=∠D．
∵∠A+∠D=90°，
∴∠A+∠GPH=90°，
∵∠A+∠ABH=90°，
∴∠ABH=∠GPH．
∵tanA=2，
∴tan∠ABH=tan∠GPH=
| 1 |
| 2 |
∴GH=
| 1 |
| 2 |
| 1 |
| 2 |
∴IB=2+1=3；
②如图2，当点I为直角顶点时，作IO⊥AD于O，
同理可以得出：△BGI≌△OPI，
∴IP=IO．
∵IO=BH=2，
∴IB=2；
③如图3，当点G为直角顶点时，
同理可以得出：△BGI≌△HPG，
∴BI=GH，GB=HP．
∵GH=
| 1 |
| 2 |
∴GH=
| 1 |
| 2 |
∴GH=
| 1 |
| 3 |
| 2 |
| 3 |
∴BI=
| 2 |
| 3 |
综上所述，IB的长度是3，2，
| 2 |
| 3 |
点评：本题考查了平行四边形的性质的运用，轴对称的性质的运用，三角形的面积公式的运用，梯形的面积公式的运用，分段函数的解法的运用，三角函数值的运用，勾股定理的运用，等腰直角三角形的性质的运用，全等三角形的判定及性质的运用，解答时寻找分段函数的分段点是难点，解答时考虑不同情况的S的值如何的表示是关键．
练习册系列答案
相关题目
17、如图，在梯形纸片ABCD中，AB∥CD，AD=BC，AB=6，CD=3．将该梯形纸片沿对角线AC折叠，点D恰与AB边上的点E重合，则∠BCE=
