题目内容
已知抛物线![]() :
:![]() (
(![]() 为常数,且
为常数,且![]() )的顶点为
)的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,其顶点为
轴对称,其顶点为![]() .若点
.若点![]() 是抛物线
是抛物线![]() 上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
解析:解:易知:C(0,1),A(m,m2+1);
若以A、B、C、P为顶点的四边形为菱形,则CP∥AB①,CP=AP②;
由①得:点P与点C纵坐标相同,将y=1代入C1,
得:x=0或x=2m,
即P(2m,1);
由②得:(2m)2=m2+(m2+1-1)2,
即m2=3,
解得m=±3;
故选A.
此题是二次函数的综合题,涉及到轴对称、菱形的性质、二次函数的性质等知识,综合性强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 。若点
。若点 是抛物线
是抛物线 (B)、
(B)、 (C)、
(C)、 (D)、
(D)、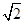
 :
: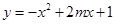 (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线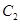 与抛物线
与抛物线 .若点
.若点 是抛物线
是抛物线
 B.
B. C.
C. D.
D.
 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 。若点
。若点 是抛物线
是抛物线 B.
B. C.
C. D.
D.
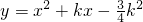 (k为常数,且k>0).
(k为常数,且k>0).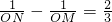 ,求k的值.
,求k的值.