摘要:20.如图.平面直角坐标系中.四边形为矩形.点的坐标分别为.动点分别从同时出发.以每秒1个单位的速度运动.其中.点沿向终点运动.点沿向终点运动.过点作.交于.连结.已知动点运动了秒. (1)点的坐标为( . )(用含的代数式表示), (2)试求面积的表达式.并求出面积的最大值及相应的值, (3)当为何值时.是一个等腰三角形?简要说明理由. 解:(1)由题意可知... 点坐标为. (2)设的面积为.在中..边上的高为.其中. . 的最大值为.此时. (3)延长交于.则有. ①若. . . . ②若.则. . ③若.则. . 在中.. .. 综上所述..或.或.
网址:http://m.1010jiajiao.com/timu3_id_454610[举报]
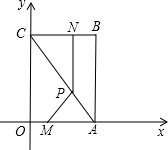 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果. 查看习题详情和答案>>
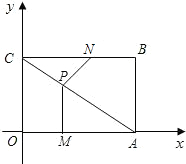 如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为多少(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由. 查看习题详情和答案>>
如图,平面直角坐标系中,四边形OABC为直角梯形,点A、B、C的坐标分别为(2,6),(8,6),(8,0).动点F、D分别从O、B同时出发,以每秒1个单位的速度运动.其中,点F沿OC向终点C运动,点D沿BA向终点A运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点D作DE⊥AB,交OB于E,连接EF.已知动点运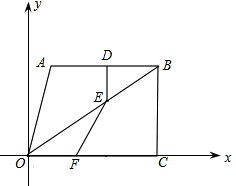 动了x秒.
动了x秒.
(1)x的取值范围为多少?
(2)E点的坐标为 ;(用含x的代数式表示)
(3)试求△OFE面积的最大值,并求此时x的值.
(4)请你探索:△OFE能否成为以OF为底边的等腰三角形?如能请求出x的值. 查看习题详情和答案>>
 动了x秒.
动了x秒.(1)x的取值范围为多少?
(2)E点的坐标为
(3)试求△OFE面积的最大值,并求此时x的值.
(4)请你探索:△OFE能否成为以OF为底边的等腰三角形?如能请求出x的值. 查看习题详情和答案>>
如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,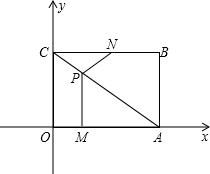 交AC于P,连接NP,已知动点运动了x秒.
交AC于P,连接NP,已知动点运动了x秒.
(1)P点的坐标为( , )(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形? 查看习题详情和答案>>
 交AC于P,连接NP,已知动点运动了x秒.
交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为(
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形? 查看习题详情和答案>>
如图,平面直角坐标系中,四边形OABC为正方形,E点在x轴的正半轴上运动,点F在CB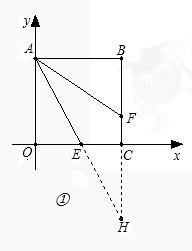 边上,且∠OAE=∠FAE
边上,且∠OAE=∠FAE
在图①中,E点在OC边上,CE=
OC,若延长AE、BC相交于点H,由∠OAE=∠FAE和AO∥BC,易知∠FAE=∠H,得AF=HF;由于E为OC中点,AO∥BC,可得△AOE≌△HCE,有AO=CH,又因AO=OC,可得CH=OC,所以有AF=CF+OC
(1)若E点在OC边上,CE=
OC,(如图②)请探索AF、FC、OC三条线段之间的数量关系,并证明你的结论;
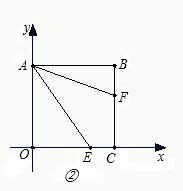
(2)若E点在OC边上,CE=
OC(n是大于1的整数),请直接写出AF、FC、OC之间的数量关系(不要求证明);
(3)若A点的坐标为(0,6),E点在x轴的正半轴上运动,点F在直线CB上,且∠OAE=∠FAE;当AF和CF相差2个单位长度时,试求出此时E点的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
 边上,且∠OAE=∠FAE
边上,且∠OAE=∠FAE在图①中,E点在OC边上,CE=
| 1 |
| 2 |
(1)若E点在OC边上,CE=
| 1 |
| 3 |
(2)若E点在OC边上,CE=
| 1 |
| n |
(3)若A点的坐标为(0,6),E点在x轴的正半轴上运动,点F在直线CB上,且∠OAE=∠FAE;当AF和CF相差2个单位长度时,试求出此时E点的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>