题目内容
如图,二次函数的图象经过点D(0,| 7 |
| 9 |
| 3 |
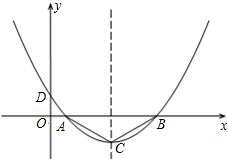 x轴上截得线段AB长为6.
x轴上截得线段AB长为6.(1)利用二次函数的对称性直接写出点A、B的坐标为
(2)求二次函数的解析式;
(3)该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;
(4)在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.
分析:(1)根据函数的对称性,又由AB=6,对称轴x=4,即可求得A,B的坐标;
(2)利用待定系数法,设二次函数的解析式为:y=a(x-h)2+k,又由抛物线过点A,B,D即可求得抛物线的解析式;
(3)由PA=PB,可知:当点P在线段DB上时PA+PD取得最小值,则可利用△BPM∽△BDO求得点P的坐标;
(4)首先求得点C的坐标,利用三角函数求得∠ACB的度数,分当点Q在x轴上方时与当点Q在x轴下方时求解即可,注意要检验是否所得结果符合题意.
(2)利用待定系数法,设二次函数的解析式为:y=a(x-h)2+k,又由抛物线过点A,B,D即可求得抛物线的解析式;
(3)由PA=PB,可知:当点P在线段DB上时PA+PD取得最小值,则可利用△BPM∽△BDO求得点P的坐标;
(4)首先求得点C的坐标,利用三角函数求得∠ACB的度数,分当点Q在x轴上方时与当点Q在x轴下方时求解即可,注意要检验是否所得结果符合题意.
解答: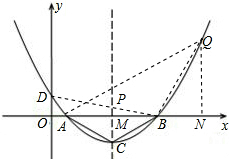 解:(1)∵对称轴为直线x=4,图象在x轴上截得的线段长为6,
解:(1)∵对称轴为直线x=4,图象在x轴上截得的线段长为6,
∴A(1,0)、B(7,0);
(2)设二次函数的解析式为:y=a(x-h)2+k,
∵顶点C的横坐标为4,且过点(0,
),
∴y=a(x-4)2+k
=16a+k①,
又∵对称轴为直线x=4,图象在x轴上截得的线段长为6,
∴A(1,0),B(7,0),
∴0=9a+k②,
由①②解得a=
,k=-
,
∴二次函数的解析式为:y=
(x-4)2-
或y=
x2-
x+
.
(3)解法一:∵点A、B关于直线x=4对称,
∴PA=PB,
∴PA+PD=PB+PD≥DB,
∴当点P在线段DB上时PA+PD取得最小值,
∴DB与对称轴的交点即为所求点P,
设直线x=4与x轴交于点M,
∵PM∥OD,
∴∠BPM=∠BDO,又∠PBM=∠DBO,
∴△BPM∽△BDO,
∴
=
,
∴PM=
=
,
∴点P的坐标为(4,
).
解法二:利用待定系数法求一次函数解析式,即直线DB为y=-
x+
.
(4)由(1)知点C(4,-
),
又∵AM=3,
∴在Rt△AMC中,cos∠ACM=
,
∴∠ACM=60°,
∵AC=BC,
∴∠ACB=120°
①当点Q在x轴上方时,过Q作QN⊥x轴于N,如果AB=BQ,
由△ACB∽△ABQ有BQ=6,∠ABQ=∠ACB=120°,则∠QBN=60°,
∴QN=3
,BN=3,ON=10,此时点Q(10,3
),如果AB=AQ,由对称性知Q(-2,3
)
②当点Q在x轴下方时,△QAB就是△ACB,此时点Q的坐标是(4,-
),
经检验,点(10,3
)与(-2,3
)都在抛物线上,
综上所述,经验证:存在这样的点Q,使△QAB∽△ABC,
点Q的坐标为(10,3
)或(-2,3
)或(4,-
).
 解:(1)∵对称轴为直线x=4,图象在x轴上截得的线段长为6,
解:(1)∵对称轴为直线x=4,图象在x轴上截得的线段长为6,∴A(1,0)、B(7,0);
(2)设二次函数的解析式为:y=a(x-h)2+k,
∵顶点C的横坐标为4,且过点(0,
| 7 |
| 9 |
| 3 |
∴y=a(x-4)2+k
| 7 |
| 9 |
| 3 |
又∵对称轴为直线x=4,图象在x轴上截得的线段长为6,
∴A(1,0),B(7,0),
∴0=9a+k②,
由①②解得a=
| ||
| 9 |
| 3 |
∴二次函数的解析式为:y=
| ||
| 9 |
| 3 |
| ||
| 9 |
8
| ||
| 9 |
7
| ||
| 9 |
(3)解法一:∵点A、B关于直线x=4对称,
∴PA=PB,
∴PA+PD=PB+PD≥DB,
∴当点P在线段DB上时PA+PD取得最小值,
∴DB与对称轴的交点即为所求点P,
设直线x=4与x轴交于点M,
∵PM∥OD,
∴∠BPM=∠BDO,又∠PBM=∠DBO,
∴△BPM∽△BDO,
∴
| PM |
| DO |
| BM |
| BO |
∴PM=
| ||||
| 7 |
| ||
| 3 |
∴点P的坐标为(4,
| ||
| 3 |
解法二:利用待定系数法求一次函数解析式,即直线DB为y=-
| ||
| 9 |
7
| ||
| 9 |
(4)由(1)知点C(4,-
| 3 |

又∵AM=3,
∴在Rt△AMC中,cos∠ACM=
| 1 |
| 2 |
∴∠ACM=60°,
∵AC=BC,
∴∠ACB=120°
①当点Q在x轴上方时,过Q作QN⊥x轴于N,如果AB=BQ,
由△ACB∽△ABQ有BQ=6,∠ABQ=∠ACB=120°,则∠QBN=60°,
∴QN=3
| 3 |
| 3 |
| 3 |
②当点Q在x轴下方时,△QAB就是△ACB,此时点Q的坐标是(4,-
| 3 |
经检验,点(10,3
| 3 |
| 3 |
综上所述,经验证:存在这样的点Q,使△QAB∽△ABC,
点Q的坐标为(10,3
| 3 |
| 3 |
| 3 |
点评:本题着重考查了待定系数法求二次函数解析式,根据函数对称性求点的坐标,以及相似三角形的判定与性质等知识.此题综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目

 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).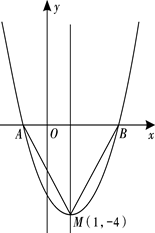
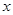 轴的交点A,B的坐标;
轴的交点A,B的坐标; 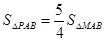 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;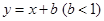 与此图象有两个公共点时,
与此图象有两个公共点时,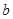 的取值范围.
的取值范围.