摘要：25．如图.DC⊥CA.EA⊥CA.DB⊥EB.DB=BE. (1)△BCD与△EAB是否全等?为什么? 解:∵DC⊥CA.EA⊥CA.DB⊥EB ∴∠C=∠A=∠DBE=90° ∵∠DBC+∠EBA+∠DBE=180° ∴∠DBC+∠EBA=90° 又∵在直角△BCD中.∠DBC+∠D=90° ∴∠D=∠EBA 在△BCD与△EAB中 ∠D=∠EBA ∠C= DB= ∴△BCD≌△EAB (2)你能说明AC = CD + AE吗?
网址：http://m.1010jiajiao.com/timu3_id_454480[举报]
24、阅读填空题：如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
求证：△BCD与△EAB全等
证明：∵DC⊥CA，EA⊥CA，DB⊥EB （已知）
∴∠C=∠A=∠DBE=90°
垂直定义
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°
直角三角形两锐角互余
∴∠D=∠EBA
等量代换
在△BCD与△EAB中
∠D=∠EBA （已证）
∠C=
∠A
（已证）DB=
BE
（已知）∴△BCD≌△EAB
AAS
．阅读填空题：
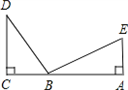
如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
求证：△BCD与△EAB全等．
证明：∵DC⊥CA，EA⊥CA，DB⊥EB （已知）
∴∠C=∠A=∠DBE=90°( )
∴∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°( )
∴∠D=∠EBA( )
在△BCD与△EAB中
∠D=∠EBA （已证）
∠C= ( )（已证）
DB=( )（已知）
∴△BCD≌△EAB( )．
查看习题详情和答案>>
如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
求证：△BCD与△EAB全等．
证明：∵DC⊥CA，EA⊥CA，DB⊥EB （已知）
∴∠C=∠A=∠DBE=90°( )
∴∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°( )
∴∠D=∠EBA( )
在△BCD与△EAB中
∠D=∠EBA （已证）
∠C= ( )（已证）
DB=( )（已知）
∴△BCD≌△EAB( )．
阅读填空题：
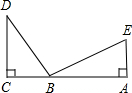
如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
求证：△BCD与△EAB全等．
证明：∵DC⊥CA，EA⊥CA，DB⊥EB（已知）
∴∠C=∠A=∠DBE=90°______
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°______
∴∠D=∠EBA______
在△BCD与△EAB中
∠D=∠EBA（已证）
∠C=______（已证）
DB=______（已知）
∴△BCD≌△EAB______．
查看习题详情和答案>>
如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
求证：△BCD与△EAB全等．
证明：∵DC⊥CA，EA⊥CA，DB⊥EB（已知）
∴∠C=∠A=∠DBE=90°______
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°______
∴∠D=∠EBA______
在△BCD与△EAB中
∠D=∠EBA（已证）
∠C=______（已证）
DB=______（已知）
∴△BCD≌△EAB______．
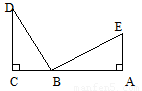
∠D=∠EBA（已证）
∠D=∠EBA（已证）