Question

阅读填空题

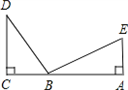
已知：如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，求证：△BCD与△EAB全等.

 

 

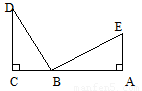
证明：∵DC⊥CA，EA⊥CA，DB⊥EB (已知)

      ∴∠C=∠A=∠DBE=90(               )

∵∠DBC+∠EBA+∠DBE=180°

∴∠DBC+∠EBA=90°

又∵在直角△BCD中，∠DBC+∠D=90°(                    )

∴∠D=∠EBA (                 )

在△BCD与△EAB中，

∠D=∠EBA（已证）

∠C=       （已证）

DB=        （已知）

∴△BCD≌△EAB(       )

 

Answer 1

【答案】

垂直的定义   三角形内角和定义    ∠A     BE     AAS

【解析】此题考查垂直的定义，三角形内角和为180°，三角形全等的判定方法。