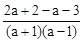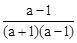摘要:(三)具体内容与考试要求细目列表 (表中“目标要求 栏中的序号和“ 具 体 内 容 知识技能要求 过程性要求 (1) (2) (3) (4) (5) (6) (7) 数 与 式 有理数的意义.用数轴上的点表示有理数 √ 相反数.绝对值的意义 √ 求相反数.绝对值.有理数的大小比较 √ 有理数加.减.乘.除.乘方及简单混合运算.运用运算律进行简化运算 √ 运用有理数的运算解决简单问题 √ 对含有较大数字的信息作出合理解释 √ 平(立)方根的概念及其表示 √ 用平方运算求某些非负数的平方根.用立方运算求某些数的立方根.用计算器求平方根与立方根 √ 无理数与实数的概念.实数与数轴上的点的一一对应关系 √ 用有理数估计一个无理数的大致范围 √ 近似数与有效数字的概念 √ 用计算器进行近似计算.并按问题的要求对结果取近似值 √ 二次根式的概念及加.减.乘.除运算法则 √ 二次根式的简单四则运算 √ 用字母表示数.列代数式表示简单数量关系 √ 代数式的实际意义与几何背景 √ 求代数式的值 √ 整数指数幂及其性质 √ 用科学记数法表示数 √ 整式的概念 √ 整式的加.减.乘(其中的多项式相乘仅指一次式相乘)运算 √ 乘法公式及计算 √ 因式分解的概念 √ 用提公因式法.公式法进行因式分解 √ 分式的概念 √ 约分.通分 √ 简单分式的运算 √ 方程与不等式 方程(组)的解的检验 √ 估计方程的解 √ 一元一次方程及解法 √ 二元一次方程组及解法 √ 可化为一元一次方程的分式方程及解法 √ 一元二次方程及其解法 √ 根据具体问题中的数量关系列方程(组)并解决实际问题 √ 根据具体问题中的数量关系列不等式(组)并解决简单实际问题 √ 不等式的基本性质 √ √ 解一元一次不等式(组) √ 用数轴表示一元一次不等式(组)的解集 √ 函 数 简单实际问题中的函数关系的分析 √ 具体问题中的数量关系及变化规律 √ 常量.变量的意义 √ 函数的概念及三种表示法 √ 简单函数的自变量取值范围.函数值 √ 使用适当的函数表示法.刻画实际问题中变量之间的关系 √ 一次函数及表达式 √ √ 一次函数的图象及性质 √ √ 正比例函数 √ 用图象法求二元一次方程组的近似解 √ 用一次函数解决实际问题 √ 反比例函数及表达式 √ √ 反比例函数的图象及性质 √ √ 用反比例函数解决实际问题 √ 二次函数及表达式 √ √ 二次函数的图象及性质 √ 确定二次函数图象的顶点.开口方向及其对称轴 √ 用二次函数解决简单实际问题 √ 用二次函数图象求一元二次方程的近似解 √ 图形的认识 点.线.面 √ 角的大小比较.估计.角的和与差的计算 √ 角的单位换算 √ 角平分线及其性质 √ 补角.余角.对顶角 √ 垂直.垂线段概念及性质.点到直线的距离 √ √ 线段垂直平分线及性质 √ 平行线的性质 √ √ 平行线间的距离 √ √ 画平行线 √ 三角形的有关概念 √ 画任意三角形的角平分线.中线.高 √ 三角形的稳定性 √ 三角形中位线的性质 √ √ 全等三角形的概念 √ 两个三角形全等的条件 √ √ 等腰三角形的有关概念 √ 等腰三角形的性质及判定 √ √ 直角三角形的概念 √ 直角三角形的性质及判定 √ √ 勾股定理及其逆定理的运用 √ √ 多边形的内角和与外角和公式 √ √ 正多边形的概念 √ 平行四边形.矩形.菱形.正方形.梯形的概念 √ 平行四边形的性质及判定 √ √ 矩形.菱形.正方形的性质及判定 √ √ 等腰梯形的有关性质和判定 √ √ 线段.矩形.平行四边形.三角形的重心及其物理意义 √ √ 平面图形的镶嵌.镶嵌的简单设计 √ 图形的认识 圆及其有关概念 √ 弧.弦.圆心角的关系 √ 点与圆.直线与圆.圆与圆的位置关系 √ √ 圆周角与圆心角的关系.直径所对圆周角的特征 √ 三角形的内心与外心 √ 切线的概念 √ 切线的性质与判定 √ √ 弧长公式.扇形面积公式 √ 圆锥的侧面积和全面积 √ 基本作图 √ 利用基本作图作三角形 √ 过平面上的点作圆 √ √ 尺规作图的步骤 √ 图形与变换 基本几何体的三视图 √ 基本几何体与其三视图.展开图之间的关系 √ 直棱柱.圆锥的侧面展开图 √ 视点.视角及盲区的涵义.及其在简单的平面图和立体图中的表示 √ 物体阴影的形成.根据光线的方向辨认实物的阴影 √ 中心投影和平行投影 √ 轴对称的基本性质 √ √ 利用轴对称作图.简单图形间的轴对称关系 √ √ 基本图形的轴对称性及其相关性质 √ 轴对称图形的欣赏与设计 √ 平移的概念.平移的基本性质 √ √ 利用平移作图.图形的欣赏与设计 √ 旋转的概念.旋转的基本性质 √ √ 平行四边形.圆的中心对称性 √ 利用旋转作图 √ 图形之间的变换关系 √ 用轴对称.平移和旋转的组合进行图案设计 √ 图形与变换 比.成比例线段.黄金分割 √ 图形的相似.相似图形的性质 √ √ 两个三角形相似的性质及判定.直角三角形相似的判定 √ √ 位似及应用 √ 相似的应用 √ 锐角三角函数 √ 特殊角的三角函数值 √ 使用计算器求已知锐角三角函数的值.由已知三角函数值求它对应的锐角 √ 三角函数的简单应用 √ 图形与坐标 平面直角坐标系,在给定的直角坐标系中.根据坐标描出点的位置.由点的位置写出它的坐标 √ 建立适当的直角坐标系描述物体的位置 √ 图形的变换与坐标的变化 √ 用不同的方式确定物体的位置 √ 图形与证明 证明的必要性 √ 定义.命题.定理.互逆命题 √ 反例的作用及反例的应用 √ 反证法的含义 √ 证明的格式及依据 √ 全等三角形的性质定理和判定定理 √ 平行线的性质定理和判定定理 √ 三角形的内角和定理及推论 √ 直角三角形全等的判定定理 √ 角平分线性质定理及逆定理 √ 垂直平分线性质定理及逆定理 √ 三角形中位线定理 √ 等腰三角形.等边三角形.直角三角形性质与判定定理 √ 平行四边形.矩形.菱形.正方形.等腰梯形的性质和判定定理 √ 统 计 数据的收集与整理.用计算器处理较复杂的统计数据 √ 总体.个体.样本的概念 √ √ 扇形统计图 √ 选择合适的统计量表示数据的集中程度 √ 加权平均数 √ 一组数据的离散程度的表示,计算极差和方差.用它们表示一组数据的离散程度 √ √ 频数.频率的概念 √ 列频数分布表.画频数分布直方图和频数折线图.并解决简单实际问题 √ 频数分布的意义和作用 √ 用样本估计总体的思想.用样本平均数.方差估计总体的平均数和方差 √ 根据统计结果作出合理的判断和预测.统计对决策的作用 √ 根据问题查找资料.获取数据信息.解决简单的实际问题 √ 概 率 概率的意义 √ 用列举法求简单事件的概率 √ 通过实验.获取事件发生的频率.大量重复实验时频率可作为事件发生概率的估计值 √ 通过实验丰富对概率的认识.并解决一些实际问题 √ 课题学习 “问题情境--建立模型--求解--解释与应用 的基本过程 √ 数学知识之间的内在联系.对数学的整体认识 √ 获得一些研究问题的方法和经验.发展思维.加深理解相关知识 √ 通过获得成功的体验和克服困难的经历.增进应用数学的自信心 √
网址:http://m.1010jiajiao.com/timu3_id_453784[举报]
爱因斯坦说过,提出一个问题比解决一个问题更重要.请你根据方程2x×3+3x=27设计一道应用题,
要求问题情景内容与我们的日常生活、学习有关,不用解答.
查看习题详情和答案>>
要求问题情景内容与我们的日常生活、学习有关,不用解答.
甲、乙两种容器的容积比是2:3,甲容器3个,乙容器1个共装水27升,求甲、乙两种容器每个的容积.
甲、乙两种容器的容积比是2:3,甲容器3个,乙容器1个共装水27升,求甲、乙两种容器每个的容积.
.如图①,在凸四边形中,∠ABC=30°,∠ADC=60°,AD=DC.
(1)如图②,若连接AC,则△ADC的形状是
答:
(2)如图③,若在四边形ABCD的外部以BC为一边作等边△BCE,并连接AE,请问:BD与AE相等吗?若相等,请加以证明;若不相等,请说明理由.
(3)在第(2)题的前提下,请你说明BD2=AB2+BC2成立的理由.

查看习题详情和答案>>
(1)如图②,若连接AC,则△ADC的形状是
等边
等边
三角形.你是根据哪个判定定理?答:
一个内角为60°的等腰三角形是等边三角形
一个内角为60°的等腰三角形是等边三角形
.(请写出定理的具体内容)(2)如图③,若在四边形ABCD的外部以BC为一边作等边△BCE,并连接AE,请问:BD与AE相等吗?若相等,请加以证明;若不相等,请说明理由.
(3)在第(2)题的前提下,请你说明BD2=AB2+BC2成立的理由.

一个不透明的袋子中放有2个红球和4个白球,它们除颜色外都相同.
(1)求从袋子中任意摸出一个球,是红球的概率是多少?
(2)不增加其它颜色的球,只允许增加一种或减少一种颜色的球,现要求从袋子中任意摸出一个球,是红球的概率为
.请你提供所有的具体的调整方案.(要求通过列式或列方程解答)
查看习题详情和答案>>
(1)求从袋子中任意摸出一个球,是红球的概率是多少?
(2)不增加其它颜色的球,只允许增加一种或减少一种颜色的球,现要求从袋子中任意摸出一个球,是红球的概率为
| 2 | 3 |
按要求化简: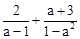 .
.
要求:见答题卡.
|
解答过程 |
解答步骤 说明 |
解题依据(用文字或符号填写知识的名称和具体内容,每空一个) |
|
|
此处不填 |
此处不填 |
|
= |
示例:通分 |
示例:分式的基本性质:分式的分子和分母都乘以同一个不等于零的整式,分式的值不变(或者“同分母分式相加减法则: |
|
= |
去括号 |
① |
|
= |
合并同类项 |
此处不填 |
|
= ② |
③ |
④ |
查看习题详情和答案>>
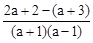
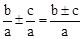 ”)
”)