摘要：8．如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O于B.C点, 则BC= ( ) A. B. C. D.
网址：http://m.1010jiajiao.com/timu3_id_453479[举报]
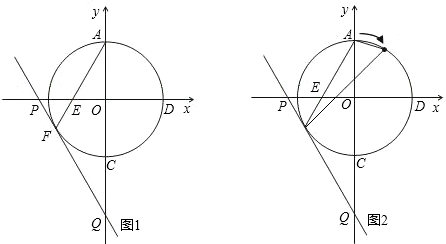
如图，在平面直角坐标系中，A点的坐标为（0，3），以O为圆心，OA为半径作圆，该圆与坐标轴分别交于A、B、C、D四点，弦AF交半径OB于点E，过点F作⊙O的切线分别交x轴、y轴于P、Q两点．
（1）求证：PE=PF；
（2）若∠FAQ=30°，求直线PQ的函数表达式；
（3）在（2）的前提下，动点M从点A出发，以
单位长度/s的速度沿
向终点F运动（如图2），设运动时间为t s，那么当t为何值时，△AMF的面积最大？最大面积是多少？
查看习题详情和答案>>
（1）求证：PE=PF；
（2）若∠FAQ=30°，求直线PQ的函数表达式；
（3）在（2）的前提下，动点M从点A出发，以
| π |
| 3 |
 |
| ADF |
查看习题详情和答案>>
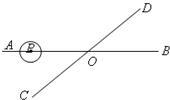15、如图，直线AB、CD相交于点O，∠AOC=30°，半径为1cm的⊙P的圆心在射线OA上，开始时，PO=6cm．如果⊙P以1cm/秒的速度沿由A向B的方向移动，那么当⊙P的运动时间t（秒）满足条件4＜t＜8
时，⊙P与直线CD相交．
如图，已知直线y=-m（x-4）（m＞0）与x轴、y轴分别交于A、B两点，以OA为直径作半圆，圆心为C．过A作x轴的垂线AT，M是线段OB上一动点（与O点不重合），过M点作半圆的切线交直线AT于N，交AB于F，切点为P．连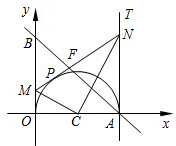
接CN、CM．
（1）证明：∠MCN=90°；
（2）设OM=x，AN=y，求y关于x的函数解析式；
（3）若OM=1，当m为何值时，直线AB恰好平分梯形OMNA的面积． 查看习题详情和答案>>
接CN、CM．（1）证明：∠MCN=90°；
（2）设OM=x，AN=y，求y关于x的函数解析式；
（3）若OM=1，当m为何值时，直线AB恰好平分梯形OMNA的面积． 查看习题详情和答案>>
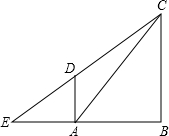相切，D为切点，AD∥BC．
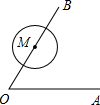如图，∠AOB=60°，点M是射线OB上的点，OM=4，以点M为圆心，2cm为半径作圆．若OA绕点O按逆时针方向旋转，当OA和⊙M相切时，OA旋转的角度是