题目内容
如图,已知直线y=-m(x-4)(m>0)与x轴、y轴分别交于A、B两点,以OA为直径作半圆,圆心为C.过A作x轴的垂线AT,M是线段OB上一动点(与O点不重合),过M点作半圆的切线交直线AT于N,交AB于F,切点为P.连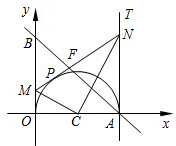 接CN、CM.
接CN、CM.(1)证明:∠MCN=90°;
(2)设OM=x,AN=y,求y关于x的函数解析式;
(3)若OM=1,当m为何值时,直线AB恰好平分梯形OMNA的面积.
分析:(1)如图推出AT,OM是⊙C的切线.得出∠CMN=
∠OMN,∠CNM=
∠ANM,根据∠CMN+∠CNM=90°,求出∠MCN;
(2)由1推出∠1=∠3,证明Rt△MOC∽Rt△CAN,利用线段比求出点A的坐标,从而求出y关于x的函数解析式;
(3)因为直线AB平分梯形ANMO的面积推出FG的长.求出直线MN的解析式后因为点F在直线MN上,易求点F的坐标.然后又因为点F在直线y=-m(x-4)求出m值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由1推出∠1=∠3,证明Rt△MOC∽Rt△CAN,利用线段比求出点A的坐标,从而求出y关于x的函数解析式;
(3)因为直线AB平分梯形ANMO的面积推出FG的长.求出直线MN的解析式后因为点F在直线MN上,易求点F的坐标.然后又因为点F在直线y=-m(x-4)求出m值.
解答:证明:(1)∵AT⊥AO,OM⊥AO,AO是⊙C的直径,
∴AT、OM是⊙C的切线,
又∵MN切⊙C于点P,
∴∠CMN=
∠OMN,∠CNM=
∠ANM,
∵OM∥AN,
∴∠ANM+∠OMN=180°,
∴∠CMN+∠CNM=
∠OMN+
∠ANM=
(∠OMN+
∠ANM)=90°,
∴∠MCN=90°;
解:(2)由(1)可知:∠1+∠2=90°,而∠2+∠3=90°,
∴∠1=∠3;
∴Rt△MOC∽Rt△CAN,
∴
=
,
∵直线y=-m(x-4)交x轴于点A,交y轴于点B,
∴0=-m(x-4),
∴x=4,
∴A(4,0),
∴AC=CO=2,
∵OM=x,AN=y,
∵
=
,
∴y=
;
(3)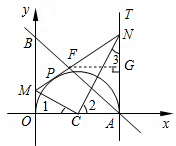
∵OM=1,
∴AN=y=4,此时S四边形ANMO=10,
∵直线AB平分梯形ANMO的面积,
∴△ANF的面积为5过点F作FG⊥AN于G,则
FG•AN=5,
∴FG=
,
∴点F的横坐标为4-
=
,
∵M(0,1),N(4,4),
∴直线MN的解析式为y=
x+1,
∵F点在直线MN上,
∴F点的纵坐标为y=
,
∴F(
,
),
∵点F又在直线y=-m(x-4)上,
∴
=-m(
-4),
∴m=
.
∴AT、OM是⊙C的切线,
又∵MN切⊙C于点P,
∴∠CMN=
| 1 |
| 2 |
| 1 |
| 2 |
∵OM∥AN,
∴∠ANM+∠OMN=180°,
∴∠CMN+∠CNM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MCN=90°;
解:(2)由(1)可知:∠1+∠2=90°,而∠2+∠3=90°,
∴∠1=∠3;
∴Rt△MOC∽Rt△CAN,
∴
| OM |
| AC |
| OC |
| AN |
∵直线y=-m(x-4)交x轴于点A,交y轴于点B,
∴0=-m(x-4),
∴x=4,
∴A(4,0),
∴AC=CO=2,
∵OM=x,AN=y,
∵
| x |
| 2 |
| 2 |
| y |
∴y=
| 4 |
| x |
(3)

∵OM=1,
∴AN=y=4,此时S四边形ANMO=10,
∵直线AB平分梯形ANMO的面积,
∴△ANF的面积为5过点F作FG⊥AN于G,则
| 1 |
| 2 |
∴FG=
| 5 |
| 2 |
∴点F的横坐标为4-
| 5 |
| 2 |
| 3 |
| 2 |
∵M(0,1),N(4,4),
∴直线MN的解析式为y=
| 3 |
| 4 |
∵F点在直线MN上,
∴F点的纵坐标为y=
| 17 |
| 8 |
∴F(
| 3 |
| 2 |
| 17 |
| 8 |
∵点F又在直线y=-m(x-4)上,
∴
| 17 |
| 8 |
| 3 |
| 2 |
∴m=
| 17 |
| 20 |
点评:本题考查的是一次函数的综合应用以及三角形的面积计算公式,难度中等.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )