网址:http://m.1010jiajiao.com/timu3_id_451999[举报]
数学课上,老师出示图和下面条件:

如图,在直角坐标平面内,O为坐标原点,A点坐标为(1,0),点B在x轴上且在点A的右侧,AB=OA.过点A和B作x轴的垂线,分别交二次函数y=x2的图像于点C和D.直线OC交BD于点M,直线CD交y轴于点H.记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH.
同学发现两个结论:①S△CMD∶S梯形ABMC=2∶3;②数值相等关系:xC·xD=-yH.
(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)
(3)进一步研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么xC、xD和yH有怎样的数值关系?(写出结果并说明理由)
查看习题详情和答案>>已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.当三角板绕点C旋转到CD与OA垂直时(如图1),易证得:OD+OE=![]() OC.当三角板绕点C旋转到CD与OA不垂直时:
OC.当三角板绕点C旋转到CD与OA不垂直时:
(1)在图2情况下上述结论仍成立,请给出证明;
(2)在图3情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.



图1 图2 图3
查看习题详情和答案>>已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.当三角板绕点C旋转到CD与OA垂直时(如图1),易证得:OD+OE=![]() OC.当三角板绕点C旋转到CD与OA不垂直时:
OC.当三角板绕点C旋转到CD与OA不垂直时:
(1)在图2情况下上述结论仍成立,请给出证明;
(2)在图3情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.



图1 图2 图3
查看习题详情和答案>>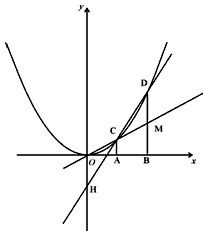
②xC·xD=-yH;
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD∶S梯形ABMC=2∶3是否仍成立?请说明理由。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么xC、xD和yH又有怎样的数量关系?写出关系式,并证明。
如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。记C、D的横坐标分别为xC,xD,点H的纵坐标yH。
(1)证明:①S△CMD∶S梯形ABMC=2∶3
②xC·xD=-yH
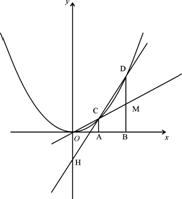
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
查看习题详情和答案>>