摘要:解:(1)连BC.则BC⊥y轴. 取DE中点M.连CM.则CM⊥x轴. ∵OD=1.OE=5.∴OM=3. ∵OB2=OD·OE=5.∴OB=. ∴圆心C.半径R=3. (2)∵△POA≌△PHE.∴PA=PE. ∵OA=OB=.OE=5.OP=a.∴. ∴ (3)解法一: 过点A作⊙C的切线AT交x正半轴于Q.设Q(m,0),则QE=m-5,QD=m-1, QT=QA-AT=QA-AB= 由OT2=OE·OD.得 ∵ ∵a=6.点P(6.0)在点Q的右侧. ∴直线AP与⊙C相离. 解法二: 设射线AP.BC交于点F.作CT⊥AF于T.则 ∵△AOP∽△CTF.∴ 而AO=.AP=.CF=BF-BC=12-3=9. ∴. ∴直线AP与⊙C相离
网址:http://m.1010jiajiao.com/timu3_id_451995[举报]
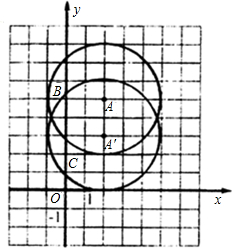 在平面直角坐标系中,以A(2,5)为圆心,以3个单位长度为半径的⊙A向下平移
在平面直角坐标系中,以A(2,5)为圆心,以3个单位长度为半径的⊙A向下平移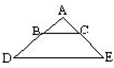 12、已知:如图,AB:BD=4:5,且DE∥BC,则BC:DE等于
12、已知:如图,AB:BD=4:5,且DE∥BC,则BC:DE等于