摘要：⑴C ⑵方法一:由题意得:A -4＜a＜0.且a≠2. ① 当2a+8＜4.即-4＜a＜-2时AC=-4-2a.BD=4-=-4-2a ∴AC=BD.当2a+8＞4.即-2＜a＜0时.同理可证:AC=BD 综上:AC=BD 方法二:①当点D在B.O之间时.连CD.∵∠COD＝90° ∴圆心M在CD上.过点D作DF∥AB.∵点M为CD中点. ∴MA为△CDF中位线.∴AC＝AF. 又DF∥AB.∴.而BO＝AO ∴AF=BD ∴AC＝BD ②点D在点B上方时.同理可证:AC=BD.综上:AC=BD ⑶方法一 ①A.D.△BDE.△ABO均为等腰直角三角形. E的纵坐标为a+6.∴ME=(yE-yM)=[a+6-(a+4)]=2.AB=4∴AB=2ME ② AM=( yM-yA)＝(a+4).BE=|yE-yB|=|a+2|. ∵AM=BE又-4＜a＜0. 且a≠2.10 当-4＜a＜-2时.(a+4)= - 20 当-2＜a＜0时.(a+4)= (a+2) ∴a不存在
网址：http://m.1010jiajiao.com/timu3_id_450667[举报]
“地震无情，人有情”，为了挽救受灾群众的生命，某地震救援队探测出某建筑物废墟下方的点
C处有生命迹象．已知废墟一侧地面上的两个探测点A、B相距3米，探测线与地面的夹角分别为30°和60°(如图)，你能确定生命所在点C的深度吗？(提示：如图，过点C作CD⊥AB交AB的延长线于点D)．
方法一：由题意知，∠
ACB＝30°．所以△ABC为________三角形．所以BC＝AB＝3米．在Rt△BDC中，∠CBD＝60°，所以CD＝BC·________≈2.6(米)．所以生命所在点
C的深度约为2.6米．方法二：因为探测线与地面的夹角分别为
30°、60°，所以∠CAD＝30°，∠CBD＝60°．在
Rt△BDC中，tan60°＝
，所以BD＝________＝________．
在
Rt△ADC中，tan30°＝
，所以AD＝________＝________．
因为
AB＝AD－BD＝3米，所以________－________＝3(米)．所以
CD＝
≈2.6(米)．
所以生命所在点
C的深度约为2.6米．26、星期天，小明见爸爸愁眉苦脸在看一张图纸，他便悄悄地来到爸爸身边，想看爸爸为什么犯愁．爸爸见到他，高兴地对他说：“来帮我一个忙，你看这是一个四边形零件的平面图，它要求∠BDC等于140°才算合格，小明通过测量得∠A=90°，∠B=19°，∠C=40°后就下结论说此零件不合格，于是爸爸让小明解释这是为什么呢？小明很轻松地说出了原因，并用如下的两种方法解出此题．请你代小明分别说出不合格的理由．
（1）如图，连接AD并延长．
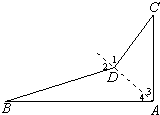
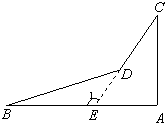
（2）如图，延长CD交AB于E．
查看习题详情和答案>>
（1）如图，连接AD并延长．
（2）如图，延长CD交AB于E．
（2012•南平）如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠1=∠B=∠C．
（1）由题设条件，请写出三个正确结论：（要求不再添加
其他字母和辅助线，找结论过程中添加的字母和辅助线不能出现在结论中，不必证明）
答：结论一：
结论二：
结论三：
（2）若∠B=45°，BC=2，当点D在BC上运动时（点D不与B、C重合），
①求CE的最大值；
②若△ADE是等腰三角形，求此时BD的长．
（注意：在第（2）的求解过程中，若有运用（1）中得出的结论，须加以证明）
查看习题详情和答案>>
（1）由题设条件，请写出三个正确结论：（要求不再添加
其他字母和辅助线，找结论过程中添加的字母和辅助线不能出现在结论中，不必证明）答：结论一：
AB=AC
AB=AC
；结论二：
∠AED=∠ADC
∠AED=∠ADC
；结论三：
△ADE∽△ACD
△ADE∽△ACD
．（2）若∠B=45°，BC=2，当点D在BC上运动时（点D不与B、C重合），
①求CE的最大值；
②若△ADE是等腰三角形，求此时BD的长．
（注意：在第（2）的求解过程中，若有运用（1）中得出的结论，须加以证明）
如图所示，小颖的家A在纬2路和经3路的十字路口，学校B在纬4路和经6路的十字路口，如果用（3，2）→（4，2）→（5，2）→（6，2）→（6，3）→（6，4）表示由A到B的一条路径，请用同样的方法写出由A到B的其他几条路径（不少于3条）．
（2012•随州）在一次数学活动课上，老师出了一道题：（1）解方程x2-2x-3=0
巡视后，老师发现同学们解此道题的方法有公式法、配方法和十字相乘法（分解因式法）．接着，老师请大家用自己熟悉的方法解第二道题：
（2）解关于x的方程mx2+（m-3）x-3=0（m为常数，且m≠0）．
老师继续巡视，及时观察、点拨大家，再接着，老师将第二道题变式为第三道题：
（3）已知关于x的函数y=mx2+（m-3）x-3（m为常数）
①求证：不论m为何值，此函数的图象恒过x轴、y轴上的两个定点（设x轴上的定点为A，y轴上的定点为C）；
②若m≠0时，设此函数的图象与x轴的另一个交点为B．当△ABC为锐角三角形时，观察图象，直接写出m的取值范围．
请你也用自己熟悉的方法解上述三道题．