摘要:已知四边形ABCD中.P是对角线BD上的一点.过P作MN∥AD.EF∥CD.分别交AB.CD.AD.BC于点M.N.E.F.设=PM·PE.=PN·PF.解答下列问题: (1)当四边形ABCD是矩形时.见图1.请判断与的大小关系.并说明理由, (2)当四边形ABCD是平行四边形.且∠A为锐角时.见图2.(1)中的结论是否成立?并说明理由, 的条件下.设.是否存在这样的实数.使得?若存在.请求出满足条件的所有的值,若不存在.请说明理由. 能力训练答案:
网址:http://m.1010jiajiao.com/timu3_id_450662[举报]
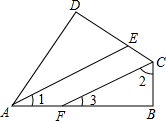 如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.填空:
如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.填空:因为∠DAB+∠DCB+∠D+∠B=360°,(
所以∠DAB+∠DCB=360°-(∠D+∠B)=180度.
因为AE平分∠DAB,CF平分∠DCB,(已知)
所以∠1=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠1+∠2=
| 1 |
| 2 |
因为∠3+∠2+∠B=180°,(
所以∠3+∠2=180°-∠B=90度.
所以∠1=∠3.(等式的性质)
所以AE∥CF.(
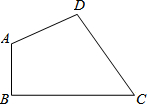 如图,已知四边形ABCD中,∠B=∠D=90°,AB=12,BC=16,则经过A、D、C三点的圆的半径为
如图,已知四边形ABCD中,∠B=∠D=90°,AB=12,BC=16,则经过A、D、C三点的圆的半径为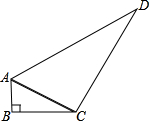 如图,已知四边形ABCD中,AB=
如图,已知四边形ABCD中,AB=
 如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=