摘要:三角函数定义: 我们规定 ①叫∠A的正弦.记作 ②叫∠A的余弦.记作 ③叫∠A的正切.记作 ④叫∠A的余切.记作 这四个三角函数定义是人们规定的,不能问为什么这样规定?这四个函数定义是本章重点中的重点,要达到①在直角三角形中,给我们一个锐角,我们知道这个角的正弦,余弦,正切,余切是哪两条线段的比.反之②在直角三角形中给我们两条线段的比,我们知道是哪个锐角的什么函数. 如图 D 再如 因为CD是∠BDC的邻边,BD是斜边,是∠BDC的邻边比斜边,所以是∠BDC的余弦. 3.特殊角的三角函数值 ①∠A=30° 此时,设 则 ②∠A=45° 此时, 则 ③∠A=60° 此时设 则 角度 函数值 30° 45° 60° 1 1
网址:http://m.1010jiajiao.com/timu3_id_450476[举报]
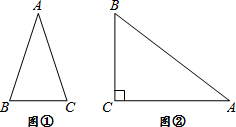 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=| BC |
| AB |
(1)sad60°=
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
(3)如图②,已知sinA=
| 3 |
| 5 |
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=| 1 |
| 2 |
根据上述对角的正对定义,解下列问题:
(1)填空:sad60°=
1
1
,sad90°=| 2 |
| 2 |
| 3 |
| 3 |
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
0<sadA<2
0<sadA<2
;(3)如图,已知sinA=
| 3 |
| 5 |
(4)设sinA=k,请直接用k的代数式表示sadA的值为
2-2
|
2-2
|
18、若我们定义a★b=4ab-a÷b,其中符号“★”是我们规定的一种运算符号,例如:6★2=4×6×2-6÷2=48-3=45,按照此关系,请计算:
(1)求(-8)★2 和(-2)★1.
(2)求9★(-3)★(-3)
查看习题详情和答案>>
(1)求(-8)★2 和(-2)★1.
(2)求9★(-3)★(-3)
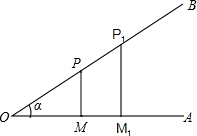 课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值
课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值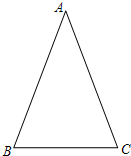 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
| 底边 |
| 腰 |
| BC |
| AB |
根据上述对角的正对定义,解下列问题:
(1)sad60°的值为( )A.
| 1 |
| 2 |
| ||
| 2 |
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
(3)已知sinα=
| 3 |
| 5 |