摘要：若方程的两实根之比是3:2,则有: A. B. C. D.
网址：http://m.1010jiajiao.com/timu3_id_449842[举报]
下面说法正确的个数是 个．
①若α、β均为锐角，且α+β=90°，sinα=
，则cosβ=
；
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
：
：1；
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+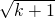
x+1=0有两个不相等的实数根，则k的取值范围是k＜且k≠0．
- A.1
- B.2
- C.3
- D.4
下面说法正确的个数是（ ）个．
①若α、β均为锐角，且α+β=90°，sinα=
，则cosβ=
；
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
：
：1；
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+
x+1=0有两个不相等的实数根，则k的取值范围是k＜
且k≠0．
①若α、β均为锐角，且α+β=90°，sinα=
| 1 |
| 3 |
2
| ||
| 3 |
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
| 3 |
| 2 |
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+
| k+1 |
| 1 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
阅读理解，回答问题．
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
与（2+
）2的大小；
（2）已知a、b为实数，且ab=1，设M=
+
，N=
+
，试比较M、N的大小；
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？ 查看习题详情和答案>>
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
| 3 |
| 3 |
（2）已知a、b为实数，且ab=1，设M=
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？ 查看习题详情和答案>>
阅读理解，回答问题．
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4与（2+）2的大小；
（2）已知a、b为实数，且ab=1，设M=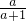
+
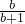，N=
+
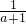，试比较M、N的大小；
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？
查看习题详情和答案>>
阅读理解，回答问题．
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
与（2+
）2的大小；
（2）已知a、b为实数，且ab=1，设M=
+
，N=
+
，试比较M、N的大小；
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？
查看习题详情和答案>>
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
| 3 |
| 3 |
（2）已知a、b为实数，且ab=1，设M=
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？