摘要:5.如图.⊙O是以AB为直径的△ABC的外接圆.点D是劣弧的中点.连 结AD并延长.与过C点的切线交于P.OD与BC相交于点E.(1)求证OE=AC, *(2)求证:=,(3)当AC=6.AB=10时.求切线PC的长. [提示](1)因为AO=BO.可证OE为△ABC的中位线.可通过证OE∥AC得到OE为中位线,(2)连结CD.则CD=BD.可转化为证明=.先证△PCD∽△PAC.得比例式=.两边平方得=.再结合切割线定理可证得==,可求DP.AP.再利用勾股定理.切割线定理可求出PC的长. (1)[略证]∵ AB为直径.∴ ∠ACB=90°. 即 AC⊥BC.∵ D为的中点.由垂径定理.得 OD⊥BC.∴ OD∥AC.又∵ 点O为AB的中点.∴ 点E为BC的中点.∴ OE=AC. *(2)[略证]连结CD.∵ ∠PCD=∠CAP.∠P是公共角.∴ △PCD∽△PAC.∴ =. ∴ =.又 PC是⊙O的切线.∴ PC2=PD·DA.∴ =. ∴ =.∵ BD=CD.∴ =. (3)[略解]在Rt△ABC中.AC=6.AB=10.∴ BC==8.∴ BE=4. ∵ OE==3.∴ ED=2.则在Rt△BED中.BD==2. 在Rt△ADB中.AD==4.∵ =.∴ =. 解此方程.得 PD=5.AP=9.又 PC2=DP·AP.∴ PC==15.
网址:http://m.1010jiajiao.com/timu3_id_449502[举报]
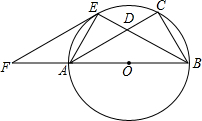 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.(1)求证:EF是⊙O切线;
(2)若AB=3,EF=2,求CD的长. 查看习题详情和答案>>
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF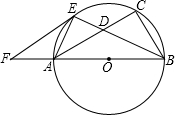 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长. 查看习题详情和答案>>
 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长. 查看习题详情和答案>>
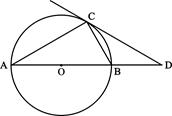
如图,⊙O是△ABC的外接圆,∠A=30°,AB是⊙O的直径,过点C作⊙O的切线,交AB延长线于D,CD=3![]() cm,
cm,
(1)求⊙O的直径。
(2)若动点M以3cm/s的速度从点A出发沿AB方向运动。同时点N以1.5cm/s的速度从B点出发沿BC方向运动。设运动的时间为t(0≤t≤2),连结MN,当t为何值时△BMN为Rt△?并求此时该三角形的面积?
查看习题详情和答案>>
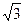 cm,
cm,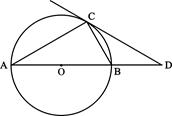
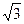 cm,
cm,