摘要:27.如图.AB为⊙O的直径.P为BA的延长线上一点.PC切⊙O于点C. CD⊥AB.垂足为D.且PA=4.PC=8.求tan ∠ACD和sin ∠P的值. [提示]连结CB.易证△PCA∽△PBC.所以=.由切割线定理可求PB的长.所以 tan∠ACD=tan ∠CBA==.连结OC.则在Rt△OCP中可求 sin∠P的值. [略解]连结OC.BC.∵ PC为⊙O的公切线.∴ PC2=PA·PB. ∴ 82=4·PB.∴ PB=16.∴ AB=16-4=12.易证△PCA∽△PBC.∴ =.∵ AB为⊙O的直径.∴ ∠ACB=90°.又 CD⊥AB.∴ ∠ACD=∠B.∴ tan ∠ACD=tan B====. ∵ PC为⊙O的切线.∴ ∠PCO=90°.∴ sin P===.
网址:http://m.1010jiajiao.com/timu3_id_449499[举报]
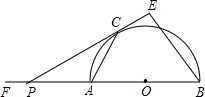 如图,AB为半圆的直径,O为圆心,AB=6,延长BA到F,使FA=AB,若P为线段AF上的一个动点(不与A重合),过P点作半圆的切线,切点为C,过B点作BE⊥PC交PC的延长线于E,设AC=x,AC+BE=y,求y与x的函数关系式及x的取值范围.
查看习题详情和答案>>
如图,AB为半圆的直径,O为圆心,AB=6,延长BA到F,使FA=AB,若P为线段AF上的一个动点(不与A重合),过P点作半圆的切线,切点为C,过B点作BE⊥PC交PC的延长线于E,设AC=x,AC+BE=y,求y与x的函数关系式及x的取值范围.
查看习题详情和答案>>
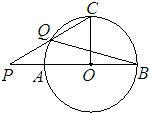 29、如图,AB为⊙O的直径,OC⊥AB,P为BA延长线上一点,PC交⊙O于点Q,若∠P=30°,则∠B=
29、如图,AB为⊙O的直径,OC⊥AB,P为BA延长线上一点,PC交⊙O于点Q,若∠P=30°,则∠B=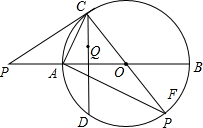 如图,AB为⊙O的直径,在BA的延长线上取点P,使PA=
如图,AB为⊙O的直径,在BA的延长线上取点P,使PA= 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.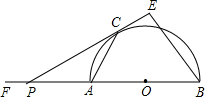 如图,AB为半圆的直径,O为圆心,AB=6,延长BA到F,使FA=AB,若P为线段AF上的一个动点(不与A重合),过P点作半圆的切线,切点为C,过B点作BE⊥PC交PC的延长线于E,设AC=x,AC+BE=y,求y与x的函数关系式及x的取值范围.
如图,AB为半圆的直径,O为圆心,AB=6,延长BA到F,使FA=AB,若P为线段AF上的一个动点(不与A重合),过P点作半圆的切线,切点为C,过B点作BE⊥PC交PC的延长线于E,设AC=x,AC+BE=y,求y与x的函数关系式及x的取值范围.