摘要:25.如图.点C.D在线段AB上.△PCD是等边三角形. (1)当AC.CD.DB满足怎样的关系时.△ACP∽△PDB? (2)当△ACP∽△PDB时.求∠APB的度数. [提示](1)考虑AC.PD.PC.DB之间比例关系. (2)利用相似三角形的性质“对应角相等 . [答案]∵ ∠ACP=∠PDB=120°. 当=.即=.也就是CD2=AC·DB时.△ACP∽△PDB. ∴ ∠A=∠DPB. ∴ ∠APB=∠APC+∠CPD+∠DPB =∠APC+∠A+∠CPD =∠PCD+∠CPD =120°. [点评]本题要求运用相似三角形判定定理和性质的运用.
网址:http://m.1010jiajiao.com/timu3_id_448895[举报]
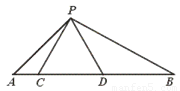
 25、如图,点C、D在线段AB上,△PCD是等边三角形.
25、如图,点C、D在线段AB上,△PCD是等边三角形.