摘要：9．如图.D是△ABC的边AB上一点.在条件(1)∠ACD＝∠B.(2)AC2＝AD·AB.(3)AB边上与点C距离相等的点D有两个.(4)∠B＝∠ACB中.一定使 △ABC∽△ACD的个数是---------------------( ) 4 [提示]由于∠A为公共角.所以考虑另一个对应角相等或∠A的两边对应成比例.才能有△ABC∽△ACD．[答案]B． [点评]本题要求运用相似三角形的判定定理．题中条件(4).∠B与∠ACB都不是 △ACD的内角.不可能成为△ABC和△ACD的对应角．由下图可见.条件(3)不一定能使△ABC∽△ACD．
网址：http://m.1010jiajiao.com/timu3_id_448879[举报]
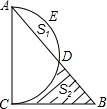如图，以△ABC的边AC为直径的半圆交AB于D，三边长a，b，c能使二次函数y=| 1 |
| 2 |
| 1 |
| 2 |
（1）证明：∠ACB=90°；
（2）若设b=2x，弓形面积S弓形AED=S1，阴影部分面积为S2，求（S2-S1）与x的函数关系式；
（3）在（2）的条件下，当b为何值时，（S2-S1）最大？ 查看习题详情和答案>>
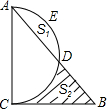
如图，以△ABC的边AC为直径的半圆交AB于D，三边长a，b，c能使二次函数y=
(c+a)x2-bx+
(c-a)的顶点在x轴上，且a是方程z2+z-20=0的一个根．
（1）证明：∠ACB=90°；
（2）若设b=2x，弓形面积S弓形AED=S1，阴影部分面积为S2，求（S2-S1）与x的函数关系式；
（3）在（2）的条件下，当b为何值时，（S2-S1）最大？
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
（1）证明：∠ACB=90°；
（2）若设b=2x，弓形面积S弓形AED=S1，阴影部分面积为S2，求（S2-S1）与x的函数关系式；
（3）在（2）的条件下，当b为何值时，（S2-S1）最大？
19、如图，在△ABC中，D是AB边上一点，连接CD．要使△ACD与△ABC相似，应添加的条件是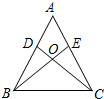
6、如图，在△ABC中，点D、E分别在边AB、AC上，BE与CD相交于点O，如果已知∠ABC=∠ACB，那么还不能判定△ABE≌△ACD，补充下列一个条件后，仍无法判定△ABE≌△ACD的是（ ）
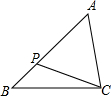如图，在△ABC中，点P是AB边上的一点，连接CP，要使△ACP∽△ABC，还需要补充的一个条件是