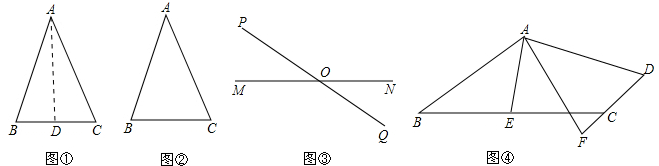
阅读与证明：在一个三角形中，如果有两个角相等，那么这两个角所对的边也相等．如图①，在△ABC中，如果∠B=∠C，那么AB=AC，这一结论可以说明如下：
解：过点A作AD⊥BC于D，则∠ADB=∠ADC=90°，在△ABD和△ACD中
∠B=∠C，∠ADB=∠ADC，AD=AD
∴△ABD≌△ACD
∴AB=AC
请你仿照上述方法在图②中再选一种方法说明以上结论．
操作：如图③，点O为线段MN的中点，直线PQ与MN相交于点O，过点M、N作一组平行线分别与PQ交于点M′、N′，则线段MM′一定等腰NN′．想一想，为什么？
根据上述阅读与证明的结论以及操作得到的经验完成下列探究活动．探究：如图④，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的等量关系，并说明你的结论．

6、有如下四个结论：
①有两边及一角对应相等的两个三角形全等；
②菱形既是轴对称图形，又是中心对称图形；
③平分弦的直径垂直于弦，并且平分弦所对的两条弧；
④两圆的公切线最多有4条．
其中正确结论的个数为（　　）

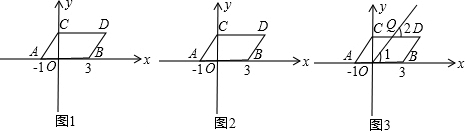
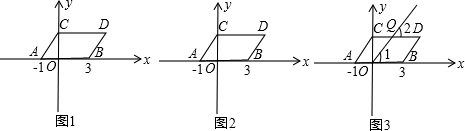
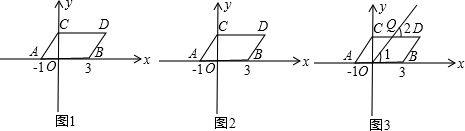
如图1，在平面直角坐标系中，点A、B的坐标分别为（-1，0）、（3，0），现将线段AB向上平移2个单位，再向右平移1个单位，得到线段CD，连接AC、BD．
（1）求点C、D的坐标及四边形ABDC的面积S_{四边形ABDC}；
（2）如图2，在y轴上是否存在一点P，连接PA、PB，使S_△PAB=S_{四边形ABDC}，若存在这样的一点，求出点P的坐标；若不存在，试说明理由．
（3）若点Q在线段CD上移动（不包括C、D两点），QO与线段CD、AB所成的角∠2与∠1如图3所示，给出下列两个结论：①∠2+∠1的值不变，②

∠1

∠2

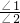的值不变，其中只有一个结论是正确的，请你找出这个结论．