摘要：解: (1)在矩形OABC中.设OC=x 则OA= x+2.依题意得 解得: ∴OC=3. OA=5 - (只要学生写出OC＝3.OA＝5即给2分) (2)连结O′D 在矩形OABC中.OC=AB.∠OCB=∠ABC=90.CE=BE= ∴ △OCE≌△ABE ∴EA=EO ∴∠1=∠2 在⊙O′中. ∵ O′O= O′D ∴∠1=∠3 ∴∠3=∠2 ∴O′D∥AE. ∵DF⊥AE ∴ DF⊥O′D 又∵点D在⊙O′上.O′D为⊙O′的半径 . ∴DF为⊙O′切线. - (3) 不同意. 理由如下: 25 当AO=AP时. 以点A为圆心.以AO为半径画弧交BC于P1和P4两点 过P1点作P1H⊥OA于点H.P1H = OC = 3.∵A P1= OA = 5 ∴A H = 4. ∴OH =1 求得点P1(1.3) 同理可得:P4 ②当OA=OP时. 同上可求得::P2(4.3).P3(4.3) -- 因此.在直线BC上.除了E点外.既存在⊙O′内的点P1.又存在⊙O′外的点P2.P3.P4.它们分别使△AOP为等腰三角形. --
网址：http://m.1010jiajiao.com/timu3_id_448124[举报]
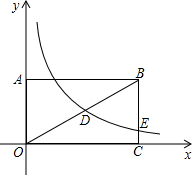（2013•本溪）如图，在矩形OABC中，AB=2BC，点A在y轴的正半轴上，点C在x轴的正半轴上，连接OB，反比例函数y=| k |
| x |
查看习题详情和答案>>
如图，在矩形OABC中，AB=2BC，点A在y轴的正半轴上，点C在x轴的正半轴上，连接OB，反比例函数y=
（k≠0，x＞0）的图象经过OB的中点D，与BC边交于点E，点E的横坐标是4，则k的值是（ ）
查看习题详情和答案>>
| k |
| x |
| A．1 | B．2 | C．3 | D．4 |
（2013•永春县质检）如图，在矩形OABC中，点A、C的坐标分别是（a，0），（0，
），点D是线段BC上的动点（与B、C不重合），过点D作直线l：y=-
x+b交线段OA于点E．
（1）直接写出矩形OABC的面积（用含a的代数式表示）；
（2）已知a=3，当直线l将矩形OABC分成周长相等的两部分时
①求b的值；
②梯形ABDE的内部有一点P，当⊙P与AB、AE、ED都相切时，求⊙P的半径．
（3）已知a=5，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，设CD=k，当k满足什么条件时，使矩形OABC和四边形O1A1B1C1的重叠部分的面积为定值，并求出该定值．
查看习题详情和答案>>
| 3 |
| 3 |
（1）直接写出矩形OABC的面积（用含a的代数式表示）；
（2）已知a=3，当直线l将矩形OABC分成周长相等的两部分时
①求b的值；
②梯形ABDE的内部有一点P，当⊙P与AB、AE、ED都相切时，求⊙P的半径．
（3）已知a=5，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，设CD=k，当k满足什么条件时，使矩形OABC和四边形O1A1B1C1的重叠部分的面积为定值，并求出该定值．
如图，在矩形OABC中，OA=8，OC=4，OA，OC分别在x，y轴上，点D在OA上，且CD=AD．