题目内容
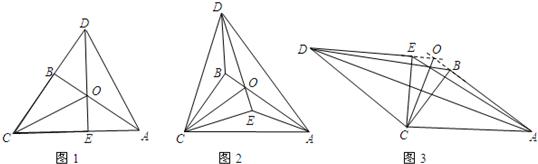
24、将两个全等的直角三角形ABC和DEC,按如图1方式放置.其中,∠ABC=∠DEC=90°,AB与DE交于点O.
(1)通过观察和测量,猜想AE、BD的数量关系为
(2)将三角形DEC绕点C逆时针旋转至图2所示的位置,(1)中的猜想是否还成立,若成立,请证明;不成立,请说明理由.
(3)将三角形DEC绕点C继续旋转至图3所示的位置,(1)中的猜想是否还成立(直接写出结论,不需证明).

(1)通过观察和测量,猜想AE、BD的数量关系为
AE=BD
;CO与AD的位置关系是CO⊥AD
;(2)将三角形DEC绕点C逆时针旋转至图2所示的位置,(1)中的猜想是否还成立,若成立,请证明;不成立,请说明理由.
(3)将三角形DEC绕点C继续旋转至图3所示的位置,(1)中的猜想是否还成立(直接写出结论,不需证明).
分析:(1)根据已知条件即可推理得出结论,(2)根据题意证明△DCB≌△ACE,根据全等三角形性质推理得出Rt△COB≌RtCOE,然后根据等腰三角形的顶角平分线的性质即可得出答案,(3)根据(2)中结论可得出答案.
解答:解:(1)AE=BD,CO⊥AD,
(2)成立,
证明:由题意可知:AD=DC,CE=CB,∠DCE=∠ACB,
∴∠DCB=∠ACE,
∴△DCB≌△ACE,
∴DB=AE,
在Rt△COB和Rt△COE中,
∵CB=CE,CO=CO,
∴Rt△COB≌RtCOE,
∴∠BCO=∠ECO,
∴∠DCO=∠ACO,
∴在等腰△ACD,CO是顶角的平分线,
∴CO⊥AD,
(3)成立.
(2)成立,
证明:由题意可知:AD=DC,CE=CB,∠DCE=∠ACB,
∴∠DCB=∠ACE,
∴△DCB≌△ACE,
∴DB=AE,
在Rt△COB和Rt△COE中,
∵CB=CE,CO=CO,
∴Rt△COB≌RtCOE,
∴∠BCO=∠ECO,
∴∠DCO=∠ACO,
∴在等腰△ACD,CO是顶角的平分线,
∴CO⊥AD,
(3)成立.
点评:本题主要考查了旋转的性质及全等三角形的证明及性质,同时考查了等腰三角形顶角平分线的性质,难度适中.

练习册系列答案
相关题目