题目内容
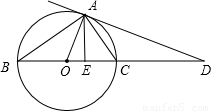
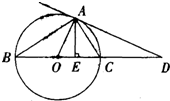 23、如图,AD切⊙O于点A,直径BC,交AD于D,AE⊥BD于E.请根据图形将线段成比例的式子写出来(至少写出4个.一个比例式和由它变形得出的比例式按一个计算).并证明其中的一个比例式成立.
23、如图,AD切⊙O于点A,直径BC,交AD于D,AE⊥BD于E.请根据图形将线段成比例的式子写出来(至少写出4个.一个比例式和由它变形得出的比例式按一个计算).并证明其中的一个比例式成立.分析:根据题意可知:①∠BAC=90°,②∠OAD=90°,③AC和AB分别是△AED内、外角的平分线,④∠DAC=∠DBA,推出Rt△ABC∽Rt△EBA∽Rt△EAC,△ABD∽△CAD,可得AB:BE=AC:AE,AB:BC=AE:AC,AC:BC=EC:AC,AB:AC=BD:AD=AD:CD,(2)由题意推出AB⊥AC,AE⊥BC,推出△ABE∽△AEC,即可推出结论.
解答:解:(一)①AB:BE=AC:AE,②AB:BC=AE:AC,③AC:BC=EC:AC,④AB:AC=BD:AD=AD:CD
(二)例:证明图1中AB:BE=AC:AE
∵BC为⊙O的直径,
∴∠BAC=90°,
∵AE⊥BC于E,
∴∠AEB=90°∠B=∠B,
∴Rt△BAC∽Rt△BEA,
∴AB:BE=AC:AE.
(二)例:证明图1中AB:BE=AC:AE
∵BC为⊙O的直径,
∴∠BAC=90°,
∵AE⊥BC于E,
∴∠AEB=90°∠B=∠B,
∴Rt△BAC∽Rt△BEA,
∴AB:BE=AC:AE.
点评:本题主要考察圆周角定理、相似三角形的判定和性质、垂径定理,解题关键在于找到图中相似的三角形.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
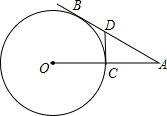 如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
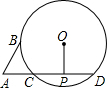 如图,AB切⊙O于点B,AD交⊙O于点C、D,OP⊥CD于点P.若AB=4cm,AD=8cm,⊙O的半径为5cm,则OP=
如图,AB切⊙O于点B,AD交⊙O于点C、D,OP⊥CD于点P.若AB=4cm,AD=8cm,⊙O的半径为5cm,则OP=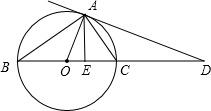 如图,AD切⊙O于点A,直径BC,交AD于D,AE⊥BD于E.请根据图形将线段成比例的式子写出来(至少写出4个.一个比例式和由它变形得出的比例式按一个计算).并证明其中的一个比例式成立.
如图,AD切⊙O于点A,直径BC,交AD于D,AE⊥BD于E.请根据图形将线段成比例的式子写出来(至少写出4个.一个比例式和由它变形得出的比例式按一个计算).并证明其中的一个比例式成立.