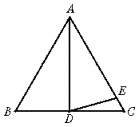
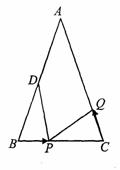
摘要：24． 如图.在△ABC中.已知AB＝BC＝CA＝4cm.AD⊥BC于D.点P.Q分别从B.C两点同时出发.其中点P沿BC向终点C运动.速度为1cm/s,点Q沿CA.AB向终点B运动.速度为2cm/s.设它们运动的时间为x(s). (1) 求x为何值时.PQ⊥AC, (2) 当0＜x＜2时.求证:AD平分△PQD的面积, (3) ①设△PQD的面积为y(cm2).求y与x的函数关系式.及自变量x的取值范围, ②△PQD的面积是否有最大值?若有.请求出这个最大值.及此时x的值,若没有.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_447534[举报]
如图，在△ABC中，已知AB＝BC＝CA＝4 cm，AD⊥BC于D．点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1 cm/s；点Q沿CA、AB向终点B运动，速度为2 cm/s．设它们运动的时间为x(s)．
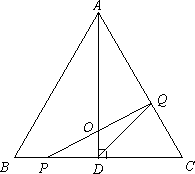
(1)求x为何值时，PQ⊥AC；
(2)设△PQD的面积为y(cm2)，当0＜x＜2时，求y与x的函数关系式；
(3)当0＜x＜2时，求证：AD平分△PQD的面积；
(4)探索以PQ为直径的圆与AC的位置关系．请写出相应位置关系的x的取值范围(不要求写出过程)．
如图，在△ABC中，AB＝3，BC＝5，AC＝7，已知线段DE＝CA，以D，E为两个顶点作位置不同的三角形，使其与△ABC全等，这样的三角形最多可画出
[ ]
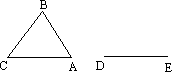
A．3个
B．4个
C．5个
D．6个
BC＝4cm,，点D为AB的中点．
