摘要:设f(x)是一次函数.f(8)=15,且f(2),f(5),f(4)成等比数列.求. 分析 本题为函数.数列.极限的一道综合题.解题关键是先利用待定系数法确定f(x)的解析式.再求f(1)+f(2)+-+f(n),然后利用极限的运算法则求极限. 解 设f(x)=kx+b, 由条件.得8k+b=15,∴b=15-8k. ∵f (2), f (5), f (4)成等比数列, ∴(5k+b)2=(2k+b)(4k+b). 2分 把b=15-8k代入. 得(15-3k)2=(15-6k)(15-4k). 解得k=4,k=0(舍),b=-17. ∴f(x)=4x-17. 4分 ∴f(1)+f(2)+-+f(n) =+-+(4×n-17) =4×(1+2+-+n)-17n =4·-17n=2n2-15n. 6分 ∴ = 8分
网址:http://m.1010jiajiao.com/timu3_id_4473480[举报]

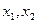 是关于
是关于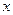 的一元二次方程
的一元二次方程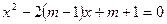 的两个实根,又
的两个实根,又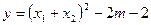 。
。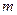 的取值范围;
的取值范围; 的解析式及最小值。
的解析式及最小值。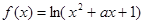 的定义域为
的定义域为 .
. ,
, ,求实数
,求实数 的范围;
的范围;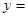
 的定义域为
的定义域为 ,求实数
,求实数 的图象在
的图象在 处的切线方程为
处的切线方程为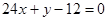 .
.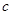 ,
,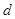 ;
;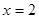 处取得极值
处取得极值 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.