题目内容
(本小题满分8分)
设A ={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
【答案】
(1)当a<-1时△<0 B=φ A;(2)当a=-1时△=0 B={0}
A;(2)当a=-1时△=0 B={0} A;(3)a≤-1或a=1。
A;(3)a≤-1或a=1。
【解析】解本题的关键是根据A∩B=B可确定 ,然后分
,然后分 和
和 两种情况进行讨论.
两种情况进行讨论.
解:A={0,—4}……………………………………2分
∵A∩B=B ∴B A……………………………………3分
A……………………………………3分
由x2+2(a+1)x+a2—1=0得
△=4(a+1)2—4(a2—1)=8(a+1)……………………………………4分
(1)当a<-1时△<0 B=φ A……………………………………5分
A……………………………………5分
(2)当a=-1时△=0 B={0} A……………………………………6分
A……………………………………6分
(3)当a>-1时△>0要使B A,则A=B
A,则A=B
∵0,-4是方程x2+2(a+1)x+a2-1=0的两根
∴
解之得a=1
综上可得a≤-1或a=1……………………………………8分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 中,
中,
 ,证明:数列
,证明:数列 是等差数列;
是等差数列; 项和
项和 .
. ,
,
 .若
.若 ,求实数
,求实数 的取值范围.
的取值范围. 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列 的前
的前 项和
项和 .
. 的前
的前
 ,
, ,当
,当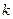 为何值时,
为何值时, 与
与 垂直?
垂直?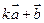 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?