摘要：用数学归纳法证明,假设n=k时,不等式成立,则当n=k+1时,应推证的目标不等式是 . 解析 因为自变量取n时,不等式的左边为n项和的形式,所以当n=k+1时应为k+1项的和,它们是,右边只需把n=k+1代入即可,它们是,故应推证的不等式是 答案
网址：http://m.1010jiajiao.com/timu3_id_4473475[举报]
,假设n=k时,不等式成立,则当n=k+1时,应推证的目标不等式是 .
,假设n=k时不等式成立,则当n=k+1时应推证的目标不等式是____________.
,假设n=k时，不等式成立，则当n=k+1时，应推证的目标是__________.
用数学归纳法证明不等式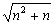
≤n+1（n∈N*），某学生的证明过程如下：
≤n+1（n∈N*），某学生的证明过程如下：（1）当n=1时，
≤1+1，不等式成立.
（2）假设n=k（k∈N*）时不等式成立，即
<k+1，则n=k+1时，
=
<
=
=（k+1）+1，
∴当n=k+1时，不等式成立.上述证法
A.过程全程正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>
用数学归纳法证明1+a+a2+…+an+1=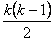
(n∈N*,a≠1)时,在验证n=1成立时,左边应为某学生在证明等差数列前n项和公式时，证法如下：
(n∈N*,a≠1)时,在验证n=1成立时,左边应为某学生在证明等差数列前n项和公式时，证法如下：(1)当n=1时，S1=a1显然成立；
(2)假设当n=k时，公式成立，即Sk=ka1+
,
当n=k+1时，Sk+1 =a1+a2+…+ak+ak+1 =a1+(a1+d)+(a1+2d)+…+［a1+(k-1)d］+(a1+kd)=(k+1)a1+(d+2d+…+kd)
=(k+1)a1+
d=(k+1)a1+
d，
∴n=k+1时公式成立.
由(1)(2)知，对n∈N*时，公式都成立.
以上证明错误的是( )
A.当n取第一个值1时，证明不对
B.归纳假设的写法不对
C.从n=k到n=k+1时的推理中未用归纳假设
D.从n=k到n=k+1时的推理有错误
查看习题详情和答案>>