摘要：数列1,,,,-,-的前n项和为Sn,则等于( ) A.0 B. C.1 D.2 分析 本题考查数列极限的求法.要求数列{an}的前n项和,应首先确定它的通项公式. 解 ∵an== ∴Sn=a1+a2+-+an=2(1-+-+-+-)=. ∴Sn=. 答案 D
网址：http://m.1010jiajiao.com/timu3_id_4473468[举报]
,
,
,…,
…的前n项和为Sn,则
等于( )
C.1 D.2
设数列{an}的前n项和为Sn，若对于任意的n∈N*，都有Sn=2an-3n．
（1）求数列{an}的首项a1与递推关系式：an+1=f（an）；
（2）先阅读下面定理：“若数列{an}有递推关系an+1=Aan+B，其中A、B为常数，且A≠1，B≠0，则数列{an-
}是以A为公比的等比数列．”请你在第（1）题的基础上应用本定理，求数列{an}的通项公式；
（3）求数列{an}的前n项和Sn． 查看习题详情和答案>>
（1）求数列{an}的首项a1与递推关系式：an+1=f（an）；
（2）先阅读下面定理：“若数列{an}有递推关系an+1=Aan+B，其中A、B为常数，且A≠1，B≠0，则数列{an-
| B | 1-A |
（3）求数列{an}的前n项和Sn． 查看习题详情和答案>>
}是以A为公比的等比数列，请你在第（1）题的基础上应用本定理，求数列{an}的通项公式;
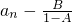是以A为公比的等比数列．”请你在第（1）题的基础上应用本定理，求数列{an}的通项公式；