摘要:20. 设M是椭圆上的一点.P.Q.T分别为M关于y轴.原点.x轴的对称点.N为椭圆C上异于M的另一点.且MN⊥MQ.QN与PT的交点为E.当M沿椭圆C运动时.求动点E的轨迹方程.
网址:http://m.1010jiajiao.com/timu3_id_4473280[举报]
(本小题满分13分)设M是椭圆![]() 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
(本小题满分13分)
已知曲线D: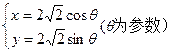 交
交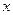 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率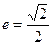 的椭圆。
的椭圆。
(1)求椭圆的标准方程;
(2)设M是直线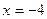 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且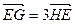 。试求此时弦PQ的长。
。试求此时弦PQ的长。
已知曲线D:
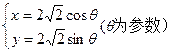 交
交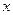 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率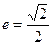 的椭圆。
的椭圆。(1)求椭圆的标准方程;
(2)设M是直线
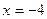 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且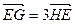 。试求此时弦PQ的长。
。试求此时弦PQ的长。(本小题满分13分)已知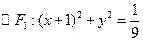 、
、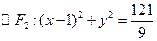 ,椭圆C的方程为
,椭圆C的方程为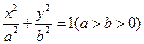 ,
,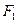 、
、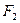 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设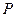 为椭圆C上一点,存在以
为椭圆C上一点,存在以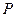 为圆心的
为圆心的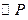 与
与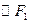 外切、与
外切、与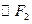 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点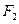 作斜率为
作斜率为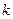 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与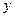 轴相交于点D,若
轴相交于点D,若
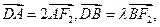 求
求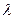 的值;
的值;
(Ⅲ)已知真命题:“如果点T(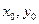 )在椭圆
)在椭圆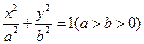 上,那么过点T
上,那么过点T
的椭圆的切线方程为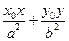 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线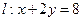 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
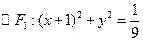 、
、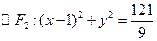 ,椭圆C的方程为
,椭圆C的方程为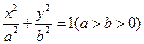 ,
,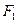 、
、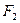 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设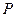 为椭圆C上一点,存在以
为椭圆C上一点,存在以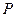 为圆心的
为圆心的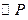 与
与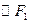 外切、与
外切、与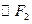 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
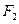 作斜率为
作斜率为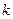 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与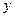 轴相交于点D,若
轴相交于点D,若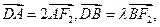 求
求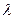 的值;
的值;(Ⅲ)已知真命题:“如果点T(
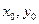 )在椭圆
)在椭圆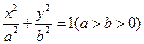 上,那么过点T
上,那么过点T的椭圆的切线方程为
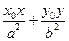 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:已知点Q是直线
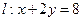 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
 是一个面积为8的正方形.
是一个面积为8的正方形.