Question

（湖南卷文）（本小题满分13分）

 已知椭圆C的中心在原点，焦点在轴上，以两个焦点和短轴的两个端点

为顶点的四边形是一个面积为8的正方形（记为Q）.

（Ⅰ）求椭圆C的方程;

（Ⅱ）设点P是椭圆C的左准线与轴的交点，过点P的直线与椭圆C相交于M,N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线的斜率的取值范围。

Answer 1

，

解析:

解 （Ⅰ）依题意，设椭圆C的方程为焦距为，

由题设条件知， 所以

故椭圆C的方程为     .

（Ⅱ）椭圆C的左准线方程为所以点P的坐标，

显然直线的斜率存在，所以直线的方程为。               

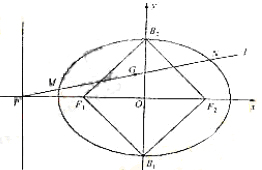
 如图，设点M，N的坐标分别为线段MN的中点为G，

     

由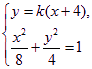得.           ……①

由解得.    ……②

因为是方程①的两根，所以，于是

=，     .

因为，所以点G不可能在轴的右边，

又直线,方程分别为

所以点在正方形内（包括边界）的充要条件为

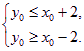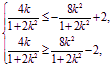 即  亦即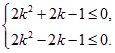                

解得，此时②也成立.      

故直线斜率的取值范围是