摘要:17.知函数(周期为. 求:当时的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_4472693[举报]
(本小题满分14分)
已知函数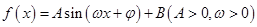 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.
查看习题详情和答案>>
、(本小题满分14分)
已知函数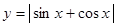
(1)画出函数在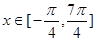 的简图;
的简图;
(2)写出函数的最小正周期和单调递增区间;并求:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状。
查看习题详情和答案>>
(本小题满分14分)
某公司2009年9月投资14400万元购得上海世界博览会某种纪念品的专利权及生产设备,生产周期为一年.已知生产每件纪念品还需要材料等其它费用20元,为保证有一定的利润,公司决定纪念品的销售单价不低于150元,进一步的市场调研还发现:该纪念品的销售单价定在150元到250元之间较为合理(含150元及250元).并且当销售单价定为150元时,预测年销售量为150万件;当销售单价超过150元但不超过200元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1万件;当销售单价超过200元但不超过250元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1.2万件.
根据市场调研结果,设该纪念品的销售单价为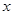 (元),年销售量为
(元),年销售量为 (万件),平均每件纪念品的利润为
(万件),平均每件纪念品的利润为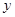 (元).
(元).
⑴求年销售量为 关于销售单价
关于销售单价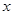 的函数关系式;
的函数关系式;
⑵该公司考虑到消费者的利益,决定销售单价不超过200元,问销售单价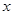 为多少时,平均每件纪念品的利润
为多少时,平均每件纪念品的利润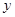 最大?
最大?
查看习题详情和答案>>
(本小题满分14分)
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |  |  |  |  |  |  |  |
 |  |  | 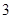 |  |  |  | 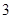 |
 的一个解析式;
的一个解析式;(2)根据(1)的结果,若函数
 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
查看习题详情和答案>>
的取值范围.
查看习题详情和答案>>








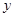



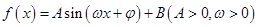 的一系列对应值如下表:
的一系列对应值如下表: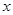
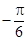
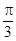
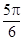
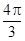
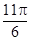
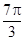
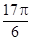
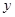
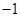
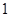
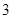
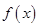 的一个解析式;
的一个解析式;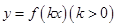 周期为
周期为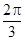 ,当
,当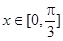 时,方程
时,方程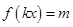 恰有两个不同的解,求实数
恰有两个不同的解,求实数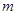 的取值范围.
的取值范围.