摘要:18.已知点A,动点P(x,y)满足 (1)求动点P的轨迹方程, 中所求轨迹与直线y=x+b交与C,D两点.且OC⊥OD,求b的值. 19参赛号码为1-5号的五名运动员参加射击比赛. (1) 通过抽签将他们安排到1-5号靶位.试求恰有一名运动员所抽靶位号与其参赛号相同的概率, (2) 记1号.2号运动员.射击的环数为ξ.(ξ所有取值为0.1.2,-,10),根据教练员提供的资料.其概率分布如下表: ξ 0 1 2 3 4 5 6 7 8 9 10 P 0 0 0 0 0.05 0.05 0.05 0.2 0.3 0.32 0.03 P 0 0 0 0 0.04 0.05 0.06 0.2 0.32 0.32 0.01 ①若1.2号运动员个射击一次.求两人中至少一人命中8环的概率, ②试判断.1号.2号运动员谁的射击水平较高?并说明理由.
网址:http://m.1010jiajiao.com/timu3_id_4472533[举报]
(本小题共12分)
如图,已知直线l与抛物线 相切于点P(2,1),且与x轴交于点A,O为坐标原点,
相切于点P(2,1),且与x轴交于点A,O为坐标原点,
定点B的坐标为(2,0).

(1)若动点M满足 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
查看习题详情和答案>>
(本小题共12分)
已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且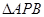 面积的最大值为
面积的最大值为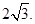
(1)求椭圆C的方程及离心率e;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。
查看习题详情和答案>>
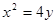 相切于点P(2,1),且与x轴交于点A,O为坐标原点,
相切于点P(2,1),且与x轴交于点A,O为坐标原点,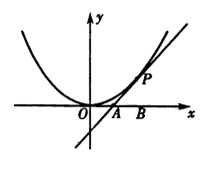
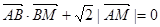 ,求点M的轨迹C;
,求点M的轨迹C; 已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且
已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且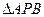 面积的最大值为
面积的最大值为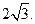
 转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。
转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。