摘要：24．取一张矩形纸进行折叠.具体操作过程如下: 第一步:先把矩形ABCD对折.折痕为MN.如图一所示. 第二步:再把B点叠在折痕线MN上.折痕为AE.点B在MN上的对应点B?.得Rt△AB?E.如图二所示. 第三步:沿EB?线折叠得折痕EF.如图三所示.利用展开图四探究. (1)△AFE是什么三角形?证明你的结论. (2)对于任一矩形.按照上述方法是否能折出这种三角形?请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_447198[举报]
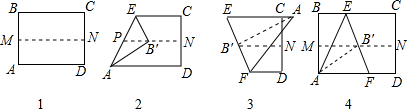
取一张矩形纸进行折叠．具体操作如下：
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′得Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，点A在直线EC上，如图（3）所示．
利用展开图（4）探究：
（1）找出图中的全等三角形；
（2）△AEF是什么三角形并证明你的结论．
查看习题详情和答案>>
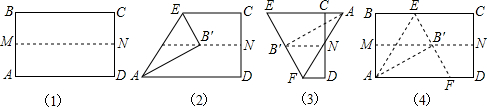
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′得Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，点A在直线EC上，如图（3）所示．
利用展开图（4）探究：
（1）找出图中的全等三角形；
（2）△AEF是什么三角形并证明你的结论．
查看习题详情和答案>>
取一张矩形纸进行折叠．具体操作如下：
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′得Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，点A在直线EC上，如图（3）所示．
利用展开图（4）探究：
（1）找出图中的全等三角形；
（2）△AEF是什么三角形并证明你的结论．
查看习题详情和答案>>
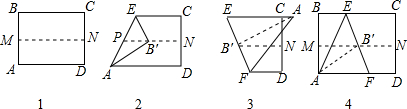
取一张矩形的纸进行折叠，具体操作过程如下：
第一步：先把矩形ABCD对折，折痕为MN，如图1；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为Bn，得Rt△ABE，如图2；
第三步：沿EB线折叠得折痕EF，如图3；
利用展开图4探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
查看习题详情和答案>>
第一步：先把矩形ABCD对折，折痕为MN，如图1；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为Bn，得Rt△ABE，如图2；
第三步：沿EB线折叠得折痕EF，如图3；
利用展开图4探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
查看习题详情和答案>>
取一张矩形的纸进行折叠，具体操作过程如下：
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得 Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，如图（3）所示；利用展开图（4）所示．
探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
（3）如图（5），将矩形纸片ABCD沿EF折叠，使点A落在DC边上的点A′处，x轴垂直平分DA，直线EF的表达式为y=kx-k （k＜0）
①问：EF与抛物线y=-
x2 有几个公共点？
②当EF与抛物线只有一个公共点时，设A′（x，y），求
的值．
查看习题详情和答案>>
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得 Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，如图（3）所示；利用展开图（4）所示．
探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
（3）如图（5），将矩形纸片ABCD沿EF折叠，使点A落在DC边上的点A′处，x轴垂直平分DA，直线EF的表达式为y=kx-k （k＜0）
①问：EF与抛物线y=-
| 1 |
| 8 |
②当EF与抛物线只有一个公共点时，设A′（x，y），求
| x |
| y |
