网址:http://m.1010jiajiao.com/timu3_id_4471887[举报]
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为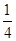 ,不堵车的概率为
,不堵车的概率为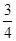 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为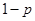 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为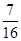 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得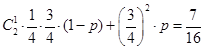
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 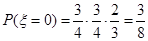 ,
, 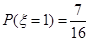
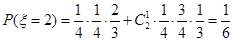 ,
,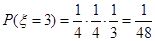
从而得到分布列和期望值
解:(I)由已知条件得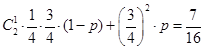 ,即
,即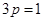 ,则
,则 的值为
的值为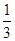 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 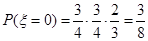 ,
, 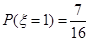
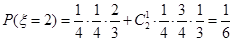 ,
,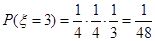
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以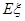
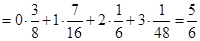
查看习题详情和答案>>
如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 的一点,
的一点, ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线 与
与 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一问中,利用建立空间直角坐标系
解:(I)以B为原点, 、
、 分别为Y,Z轴建立空间直角坐标系.由于,
分别为Y,Z轴建立空间直角坐标系.由于,

在三棱柱 中有
中有
 ,
,
设


又 侧面
侧面 ,故
,故 . 因此
. 因此 是异面直线
是异面直线 的公垂线,则
的公垂线,则 ,故异面直线
,故异面直线 的距离为1.
的距离为1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小为向量
的大小为向量 与
与 的夹角.
的夹角.

查看习题详情和答案>>
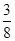
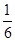
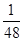
 满足
满足 ,试判定
,试判定 ,
,
 ,
, ,
, 是直角三角形.
是直角三角形.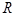 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于

 ,
, ,数列
,数列 的项满足:
的项满足: ,(1)试求
,(1)试求
 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明. ,
, 
 ,
, 
 然后再用数学归纳法分为两步骤证明即可。
然后再用数学归纳法分为两步骤证明即可。 ,
,
 ,命题成立
,命题成立 时,
时, 成立
成立 时,
时,

