摘要： 设.为常数.:把平面上任意一点 (.)映射为函数 (1)证明:不存在两个不同点对应于同一个函数, (2)证明:当时..这里t为常数, (3)对于属于M的一个固定值.得.在映射F的作用下.M1作为象.求其原象.并说明它是什么图象? 答案:
网址：http://m.1010jiajiao.com/timu3_id_4471482[举报]
设a、b为常数，M＝{f(x)|f(x)＝acosx＋bsinx}；F：把平面上任意一点(a，b)映射为函数acosx＋bsinx．
(1)证明：不存在两个不同点对应于同一个函数；
(2)证明：当f0(x)∈M时，f1(x)＝f0(x＋t)∈M，这里t为常数；
(3)对于属于M的一个固定值f0(x)，得M1＝{f0(x＋t)，t∈R}，在映射F的作用下，M1作为象，求其原象，并说明它是什么图象？
设a、b为常数，M={f（x）|f（x）=acosx+bsinx，x∈R}；F：把平面上任意一点（a，b）映射为函数acosx+bsinx．
（1）证明：对F不存在两个不同点对应于同一个函数；
（2）证明：当f0（x）∈M时，f1（x）=f0（x+t）∈M，这里t为常数；
（3）对于属于M的一个固定值f0（x），得M1={f0（x+t）|t∈R}，若映射F的作用下点（m，n）的象属于M1，问：由所有符合条件的点（m，n）构成的图形是什么？
查看习题详情和答案>>
（1）证明：对F不存在两个不同点对应于同一个函数；
（2）证明：当f0（x）∈M时，f1（x）=f0（x+t）∈M，这里t为常数；
（3）对于属于M的一个固定值f0（x），得M1={f0（x+t）|t∈R}，若映射F的作用下点（m，n）的象属于M1，问：由所有符合条件的点（m，n）构成的图形是什么？
设a、b为常数，M={f（x）|f（x）=acosx+bsinx，x∈R}；F：把平面上任意一点（a，b）映射为函数acosx+bsinx．
（1）证明：对F不存在两个不同点对应于同一个函数；
（2）证明：当f（x）∈M时，f1（x）=f（x+t）∈M，这里t为常数；
（3）对于属于M的一个固定值f（x），得M1={f（x+t）|t∈R}，若映射F的作用下点（m，n）的象属于M1，问：由所有符合条件的点（m，n）构成的图形是什么？
查看习题详情和答案>>
（1）证明：对F不存在两个不同点对应于同一个函数；
（2）证明：当f（x）∈M时，f1（x）=f（x+t）∈M，这里t为常数；
（3）对于属于M的一个固定值f（x），得M1={f（x+t）|t∈R}，若映射F的作用下点（m，n）的象属于M1，问：由所有符合条件的点（m，n）构成的图形是什么？
查看习题详情和答案>>
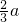，P到一条准线的距离是
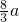，则此椭圆的离心率为
．
（a≠b，且a，b为正的常数）的准线上任意一点到两焦点的距离分别为d1，d2，则|d12-d22|为定值．