题目内容
设a、b为常数,M={f(x)|f(x)=acosx+bsinx,x∈R};F:把平面上任意一点(a,b)映射为函数acosx+bsinx.(1)证明:对F不存在两个不同点对应于同一个函数;
(2)证明:当f(x)∈M时,f1(x)=f(x+t)∈M,这里t为常数;
(3)对于属于M的一个固定值f(x),得M1={f(x+t)|t∈R},若映射F的作用下点(m,n)的象属于M1,问:由所有符合条件的点(m,n)构成的图形是什么?
【答案】分析:(1)假设有两个不同的点(a,b),(c,d)对应同一函数,即acosx+bsinx=ccosx+dsinx对一切实数x均成立.特别令x=0,得a=c;令x= ,得b=d.这与(a,b),(c,d)是两个不同点矛盾,故不存在两个不同点对应同函数.
,得b=d.这与(a,b),(c,d)是两个不同点矛盾,故不存在两个不同点对应同函数.
(2)当f(x)∈M时,可得常数aa,b,使f(x)=acosx+bsinx,f1(x)=f(x+t)=acos(x+t)+bsin(x+t)=(acost+bsint)+(bcost-asint)sinx.由此能够证明f1(x)=f(x+t)∈M.
(3)设f(x)∈M,由此得f(x+t)=mcosx+nsinx,在映射F下,f(x+t)的原象是(m,n),则M1的原象是{(m,n)|m=acost+bsint,n=bcost-asint,t∈R},消去t得m2+n2=a2+b2,由此能得到有符合条件的点(m,n)构成的图形是圆.
解答:解:(1)证明:假设有两个不同的点(a,b),(c,d)对应同一函数,
即F(a,b)=acosx+bsinx与F(c,d)=ccosx+dsinx相同,
即acosx+bsinx=ccosx+dsinx对一切实数x均成立.
特别令x=0,得a=c;
令x=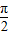 ,得b=d.
,得b=d.
这与(a,b),(c,d)是两个不同点矛盾,
假设不成立.
故不存在两个不同点对应同函数.
(2)当f(x)∈M时,
可得常数aa,b,使f(x)=acosx+bsinx,
f1(x)=f(x+t)=acos(x+t)+bsin(x+t)
=(acost+bsint)+(bcost-asint)sinx.
由于a,b,t为常数,
设acost+bsint=m,bcost-asint=n,
则m,n是常数.
从而f1(x)=f(x+t)∈M.
(3)设f(x)∈M,
由此得f(x+t)=mcosx+nsinx,
(其中m=acost+bsint,n=bcost-asint)
在映射F下,f(x+t)的原象是(m,n),
则M1的原象是
{(m,n)|m=acost+bsint,n=bcost-asint,t∈R},
消去t得m2+n2=a2+b2,
即在映射F下,M1的原象{(m,n)|m2+n2=a2+b2}是以原点为圆心,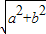 为半径的圆.
为半径的圆.
点评:本题考查映射的概念,难度较大.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,得b=d.这与(a,b),(c,d)是两个不同点矛盾,故不存在两个不同点对应同函数.
,得b=d.这与(a,b),(c,d)是两个不同点矛盾,故不存在两个不同点对应同函数.(2)当f(x)∈M时,可得常数aa,b,使f(x)=acosx+bsinx,f1(x)=f(x+t)=acos(x+t)+bsin(x+t)=(acost+bsint)+(bcost-asint)sinx.由此能够证明f1(x)=f(x+t)∈M.
(3)设f(x)∈M,由此得f(x+t)=mcosx+nsinx,在映射F下,f(x+t)的原象是(m,n),则M1的原象是{(m,n)|m=acost+bsint,n=bcost-asint,t∈R},消去t得m2+n2=a2+b2,由此能得到有符合条件的点(m,n)构成的图形是圆.
解答:解:(1)证明:假设有两个不同的点(a,b),(c,d)对应同一函数,
即F(a,b)=acosx+bsinx与F(c,d)=ccosx+dsinx相同,
即acosx+bsinx=ccosx+dsinx对一切实数x均成立.
特别令x=0,得a=c;
令x=
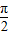 ,得b=d.
,得b=d.这与(a,b),(c,d)是两个不同点矛盾,
假设不成立.
故不存在两个不同点对应同函数.
(2)当f(x)∈M时,
可得常数aa,b,使f(x)=acosx+bsinx,
f1(x)=f(x+t)=acos(x+t)+bsin(x+t)
=(acost+bsint)+(bcost-asint)sinx.
由于a,b,t为常数,
设acost+bsint=m,bcost-asint=n,
则m,n是常数.
从而f1(x)=f(x+t)∈M.
(3)设f(x)∈M,
由此得f(x+t)=mcosx+nsinx,
(其中m=acost+bsint,n=bcost-asint)
在映射F下,f(x+t)的原象是(m,n),
则M1的原象是
{(m,n)|m=acost+bsint,n=bcost-asint,t∈R},
消去t得m2+n2=a2+b2,
即在映射F下,M1的原象{(m,n)|m2+n2=a2+b2}是以原点为圆心,
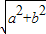 为半径的圆.
为半径的圆.点评:本题考查映射的概念,难度较大.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
设a,b为常数,M{f(x)|f(x)=acosx+bsinx};F:把平面上任意一点(a,b)映射为函数acodx+bsinx.
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当f0(x)ÎM时,f1(x)=f0(x+t)ÎM,这里t为常数;
(3)对于属于M的一个固定值f0(x),得M1={f0(
设a、b为常数,M={f(x)|f(x)=acosx+bsinx};F:把平面上任意一点(a,b)映射为函数acosx+bsinx. (1)证明:不存在两个不同点对应于同一个函数; (2)证明:当f0(x)∈M时,f1(x)=f0(x+t)∈M,这里t为常数; (3)对于属于M的一个固定值f0(x),得M1={f0(x+t),t∈R},在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?