摘要:若 (I)求f (x)的最小正周期, (II)记g(x)=2f (x)+a的最小值为-2.求实数a的值. 已知圆C的参数方程为(θ为参数.且θ∈[0, 2π)).且圆C与直线l1: x+y-1=0的两个交点为P.Q.若(O为坐标原点). (I)求实数a的值, (II)若a≠0.直线l2与l1有相同的方向向量.且截圆C所得弦长是1.求直线l2的方程. 甲.乙两个独立地破译一个密码.甲能译出的概率为.乙能译出的概率为x.甲.乙两人中至少有一人能译出的概率为y.恰有一人能译出的概率为. (I)求x, y的值, (II)求甲.乙两人都译不出的概率. 已知函数.数列{an}的首项为.前n项和为sn.且当n≥2时.sn=f (sn-1). (I)证明:数列是等差数列.并求出sn的表达式, (II)设.求数列{bn}的前n项和Tn. 已知函数上为增函数. (I)求实数a的取值范围, (II)设f (x)的导函数为f ′(x), g(x)=sinx+cosx-1, a取(1)中的最小值.求证:当x>0时.g(x)>f ′(x). 已知两点M, N.动点P在y轴上的射影是H.若存在常数m使.m+2, m成等差数列. (I)求动点P的轨迹C的方程, (II)当m∈[-4, 0]时.讨论动点P的轨迹是什么图形? (III)当m=-2时.过点N的直线l交曲线C于x轴下方两个不同点A.B.设R为AB中点.若过点R与点Q的直线交x轴于点D(x0, 0).求x0的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_4471173[举报]
(本小题满分12分)
已知直线l1:4x:-3y+6=0和直线l2:x=-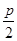 ,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程;
(II)直线l过抛物线C的焦点F与抛物线交于A,B两点,且AA1,BB1都垂直于直线l2,垂足为A1,B1,直线l2与y轴的交点为Q,求证: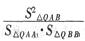 为定值。
为定值。
查看习题详情和答案>>
(本小题满分12分)
已知向量 a = (cos x,sin x),b = (-cos x,cos x),c = (-1,0)
(I) 若 x = ,求向量 a、c 的夹角;
(II) 当 x∈[,] 时,求函数 f (x) = 2a·b + 1 的最大值。
查看习题详情和答案>>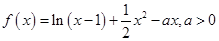 .
.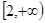 的最小值为f(t),求t的值。
的最小值为f(t),求t的值。 cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于
cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于 .
. 当ω取最大值时,f(A)=1,求△ABC的面积.
当ω取最大值时,f(A)=1,求△ABC的面积.