题目内容
(本小题满分12分)
已知直线l1:4x:-3y+6=0和直线l2:x=-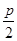 ,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程;
(II)直线l过抛物线C的焦点F与抛物线交于A,B两点,且AA1,BB1都垂直于直线l2,垂足为A1,B1,直线l2与y轴的交点为Q,求证: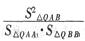 为定值。
为定值。
【答案】
(Ⅰ)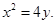 (Ⅱ)
(Ⅱ)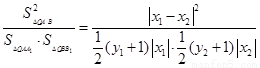 =
=
【解析】
试题分析:(Ⅰ)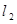 为抛物线的准线,焦点为
为抛物线的准线,焦点为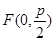 ,由抛物线的定义知,抛物线上的点到直线
,由抛物线的定义知,抛物线上的点到直线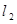 的距离等于其到焦点
的距离等于其到焦点 的距离,
的距离,
抛物线上的点到直线 的距离与到焦点
的距离与到焦点 的距离之和的最小值为焦点
的距离之和的最小值为焦点 到直线
到直线 的距离
的距离 ……3分
……3分
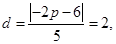 所以
所以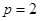 ,
,
所以抛物线的方程为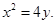 ……………5分
……………5分
(Ⅱ)设 ,
, ,
,
设: ,则
,则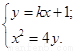
得
所以 ,
, ,
,
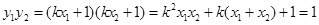 ,
,
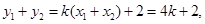 ……………7分
……………7分
又
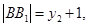

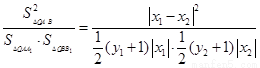 ………………10分
………………10分
 =
= ……………12分
……………12分
考点:本题主要考查抛物线的标准方程,抛物线的几何意义,直线与抛物线的位置关系。
点评:中档题,本题求抛物线的标准方程,主要运用的是抛物线的几何性质,注意明确焦点轴和p的值。研究直线与抛物线的位置关系,往往应用韦达定理,通过“整体代换”,简化解题过程,实现解题目的。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目