��Ŀ����
 ��ͼ��һ����������ʾ��ͼ������ABCD�DZ߳�Ϊ2a�������Σ���Χ���ĸ�ȫ�ȵĹ��Σ���֪OΪ�����ε����ģ�GΪAD���е㣬��P��ֱ��OG�ϣ���AD����PΪԲ�ġ�PAΪ�뾶��Բ��һ���֣�OG���ӳ��߽���AD�ڵ�H���軡AD�ij�Ϊl����APH=�ȣ��ȡ�(
��ͼ��һ����������ʾ��ͼ������ABCD�DZ߳�Ϊ2a�������Σ���Χ���ĸ�ȫ�ȵĹ��Σ���֪OΪ�����ε����ģ�GΪAD���е㣬��P��ֱ��OG�ϣ���AD����PΪԲ�ġ�PAΪ�뾶��Բ��һ���֣�OG���ӳ��߽���AD�ڵ�H���軡AD�ij�Ϊl����APH=�ȣ��ȡ�(| �� |
| 4 |
| 3�� |
| 4 |
| OP |
| l |
| �� |
| 4 |
��������1���ȶԦ����ڷ�Χ�������⣬����ۺϼ��ɣ�
��2���ȸ����������OP=a-
���ȡʣ�
��
���������õ�
=
��Ȼ�������������������������ֵ�㼴�ɵõ����ۣ�
��2���ȸ����������OP=a-
| acos�� |
| sin�� |
| �� |
| 4 |
| 3�� |
| 4 |
| OP |
| L |
| sin��-cos�� |
| 2�� |
����⣺��1�����ȡʣ�
��
��ʱ����P���߶�OG�ϣ�AP=
��
���ȡʣ�
��
��ʱ����P���߶�GH�ϣ�AP=
=
��
����=
ʱ��AP=a��
��������AP=
���ȡʣ�
��
����
���ԣ���AD�ij�L=AP•2��=
��
����������ϵʽΪL=
���ȡʣ�
��
����
��2��֤�������ȡʣ�
��
��ʱ��OP=OG-PG=a-
=a-
��
���ȡʣ�
��
��ʱ��OP=OG+GH=a+
=a-
=a-
��
����=
ʱ��OP=a��
���ԣ�OP=a-
���ȡʣ�
��
����
�Ӷ���
=
���ȡʣ�
��
����
��f���ȣ�=
���ȡʣ�
��
����
��f�䣨�ȣ�=
��f�䣨�ȣ�=0�æȣ�cos��+sin�ȣ�=sin��-cos��
��Ϊ�ȡʣ�
��
������cos��+sin�ȡ�0���Ӷ���=
��
��Ȼ�ȡ�
�����Ԧ�=
=
=tan����-
��
�������=tan����-
���Ħ�=��0������֤����0�Ǻ���f���ȣ��ļ�ֵ�㣮
��g���ȣ�=�ȣ�cos��+sin�ȣ�-��sin��-cos�ȣ����ȡʣ�
��
����
��g�䣨�ȣ�=�ȣ�cos��-sin�ȣ���0�Ϧȡʣ�
��
���������
�Ӷ�g���ȣ��ڦȡʣ�
��
���ϵ����ݼ���
���ԣ����ȡʣ�
����0��ʱg���ȣ���0����f�䣨�ȣ���0��f���ȣ��ڣ�
����0���ϵ���������
���ȡʣ���0��
��ʱ��g���ȣ���0����f�䣨�ȣ���0��f���ȣ��ڣ���0��
���ϵ����ݼ���
��f���ȣ��ڦ�=��0����ȡ�ü���ֵҲ�����ֵ��
���ԣ����������=tan����-
��ʱ������f���ȣ���
ȡ�����ֵ����ʱ��������������
| �� |
| 4 |
| �� |
| 2 |
| a |
| sin�� |
���ȡʣ�
| �� |
| 2 |
| 3�� |
| 4 |
| a |
| sin(��-��) |
| a |
| sin�� |
����=
| �� |
| 2 |
��������AP=
| a |
| sin�� |
| �� |
| 4 |
| 3�� |
| 4 |
���ԣ���AD�ij�L=AP•2��=
| 2a�� |
| sin�� |
����������ϵʽΪL=
| 2a�� |
| sin�� |
| �� |
| 4 |
| 3�� |
| 4 |
��2��֤�������ȡʣ�
| �� |
| 4 |
| �� |
| 2 |
| a |
| tan�� |
| acos�� |
| sin�� |
���ȡʣ�
| �� |
| 2 |
| 3�� |
| 4 |
| a |
| tan(��-��) |
| a |
| tan�� |
| acos�� |
| sin�� |
����=
| �� |
| 2 |
���ԣ�OP=a-
| acos�� |
| sin�� |
| �� |
| 4 |
| 3�� |
| 4 |
�Ӷ���
| OP |
| L |
| sin��-cos�� |
| 2�� |
| �� |
| 4 |
| 3�� |
| 4 |
��f���ȣ�=
| sin��-cos�� |
| 2�� |
| �� |
| 4 |
| 3�� |
| 4 |
��f�䣨�ȣ�=
| ��(cos��+sin��)-(sin��-cos��) |
| 2��2 |
��f�䣨�ȣ�=0�æȣ�cos��+sin�ȣ�=sin��-cos��
��Ϊ�ȡʣ�
| �� |
| 4 |
| 3�� |
| 4 |
| sin��-cos�� |
| sin��+cos�� |
��Ȼ�ȡ�
| �� |
| 2 |
| sin��-cos�� |
| sin��+cos�� |
| tan��-1 |
| tan��+1 |
| �� |
| 4 |
�������=tan����-
| �� |
| 4 |
��g���ȣ�=�ȣ�cos��+sin�ȣ�-��sin��-cos�ȣ����ȡʣ�
| �� |
| 4 |
| 3�� |
| 4 |
��g�䣨�ȣ�=�ȣ�cos��-sin�ȣ���0�Ϧȡʣ�
| �� |
| 4 |
| 3�� |
| 4 |
�Ӷ�g���ȣ��ڦȡʣ�
| �� |
| 4 |
| 3�� |
| 4 |
���ԣ����ȡʣ�
| �� |
| 4 |
| �� |
| 4 |
���ȡʣ���0��
| 3�� |
| 4 |
| 3�� |
| 4 |
��f���ȣ��ڦ�=��0����ȡ�ü���ֵҲ�����ֵ��
���ԣ����������=tan����-
| �� |
| 4 |
| OP |
| L |
������������Ҫ������������������е�Ӧ�����⣮�������ĵڶ���ʱ�漰��������������������ֵ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
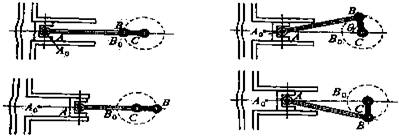

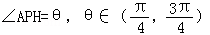 ��
��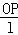 Ϊ������������ϵ����������ϵ�����ʱ����������������֤�������Ǧ����㣺
Ϊ������������ϵ����������ϵ�����ʱ����������������֤�������Ǧ����㣺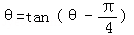 ʱ����������������
ʱ����������������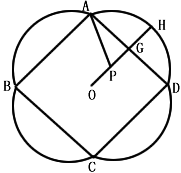
 ����1����l���ڦȵĺ�����ϵʽ����2�������ֵ
����1����l���ڦȵĺ�����ϵʽ����2�������ֵ Ϊ������������ϵ����������ϵ�����ʱ����������������֤�������Ǧ����㣺
Ϊ������������ϵ����������ϵ�����ʱ����������������֤�������Ǧ����㣺 ʱ����������������
ʱ����������������