Question

 （08年扬州中学） 如图，在四棱锥P―ABC中，PA⊥底面ABCD，∠DAB=90°，AB∥CD，AD=CD=2AB=2，E、F分别为PC、CD的中点

    ⑴证明：CD⊥平面BEF；

⑵设PA=k?AB，且AD与PC所成的角为60°，求k的值．

 

Answer 1

解析：⑴  矩形ABFD，∴

E、F分别为PC、CD的中点PD∥EF，

∴

⑵延长AB到G使BG=AB，则AG=CD且AG∥CD，∠DAB=90°，

∴四边形AGCD是矩形，有CG∥AD，∴∠PCG为AD与PC所成的角，即∠PCG=60°

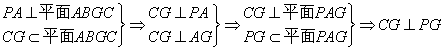
∵PA⊥AG，PA=k，AG=2，∴PG=，CG=AD=2

∴，K＝