题目内容
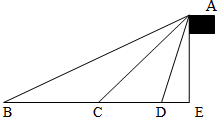 高一某班研究性小组成员为了测量永嘉中学旗杆高度收集了如下数据:(如图)在B点测得∠ABE=θ,前进30米至C点处,测得∠ACE=2θ,再继续前进10
高一某班研究性小组成员为了测量永嘉中学旗杆高度收集了如下数据:(如图)在B点测得∠ABE=θ,前进30米至C点处,测得∠ACE=2θ,再继续前进10| 3 |
| π |
| 12 |
| π |
| 12 |
15
15
米.分析:由题意及仰角的定义,利用数形结合的思想,利用图形中角与角的联系及三角形求解即可.
解答:解:由已知BC=30米,CD=10
米,∠ABE=θ,
∠ACE=2θ,∠ADE=4θ,
在Rt△ABCE中,BE=AEcotθ,
在Rt△ACE中,CE=AEcot2θ,
∴BC=BE-CE=AE(cotθ-cot2θ).
同理可得:CD=AE(cot2θ-cot4θ).
∴
=
,
即
=
=
,
而cotθ-cot2θ=
-
=
=
.
同理可得cot2θ-cot4θ=
.
=
=2cos2θ=
,
∴cos2θ=
,结合题意可知:2θ=30°,θ=15°,
∴AE=
=BCsin2θ=15(米).
故答案为:
;15.
| 3 |
∠ACE=2θ,∠ADE=4θ,
在Rt△ABCE中,BE=AEcotθ,
在Rt△ACE中,CE=AEcot2θ,
∴BC=BE-CE=AE(cotθ-cot2θ).
同理可得:CD=AE(cot2θ-cot4θ).
∴
| BC |
| DC |
| AE(cotθ-cot2θ) |
| AE(cot2θ-cot2θ) |
即
| cotθ-cot2θ |
| cot2θ-cot4θ |
| 30 | ||
10
|
| 3 |
而cotθ-cot2θ=
| cotθ |
| sinθ |
| cos2θ |
| sin2θ |
=
| sin2θcosθ-cos2θsinθ |
| sinθsin2θ |
| 1 |
| sin2θ |
同理可得cot2θ-cot4θ=
| 1 |
| sin4θ |
| cotθ-cot2θ |
| cot2θ-cot4θ |
| sin4θ |
| cos2θ |
| 3 |
∴cos2θ=
| ||
| 2 |
∴AE=
| BC |
| cotθ-cot2θ |
故答案为:
| π |
| 12 |
点评:本题以实际问题为载体,考查了学生会从题意中抽取出图形进而分析问题,还考查了学生们利用三角形解出三角形的边与角,及二倍角的正切公式.

练习册系列答案
相关题目
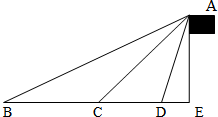 高一某班研究性小组成员为了测量永嘉中学旗杆高度收集了如下数据:(如图)在B点测得∠ABE=θ,前进30米至C点处,测得∠ACE=2θ,再继续前进10
高一某班研究性小组成员为了测量永嘉中学旗杆高度收集了如下数据:(如图)在B点测得∠ABE=θ,前进30米至C点处,测得∠ACE=2θ,再继续前进10 米至点D处,测得∠ADE=4θ,则θ的大小为________,旗杆AE的高度为________米.
米至点D处,测得∠ADE=4θ,则θ的大小为________,旗杆AE的高度为________米.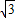 米至点D处,测得∠ADE=4θ,则θ的大小为 ,旗杆AE的高度为 米.
米至点D处,测得∠ADE=4θ,则θ的大小为 ,旗杆AE的高度为 米.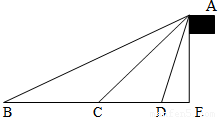
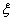 ,且
,且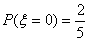 ,求:
,求: