摘要:19.解:⑴ 当时.有.是偶函数 2分 由得. 又得. 5分 6分 ⑵ 当时.有. 任取且 8分 . 即 在上是减函数. 10分 ⑶ 由于在上是减函数.在上是减函数 当时.有. 当时.有. 当时.有. 13分 当时.方程在上有实数解. 14分
网址:http://m.1010jiajiao.com/timu3_id_4470822[举报]
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形![]() 中,已知过点
中,已知过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() 。若
。若![]() 。
。
(1)求证:![]() 与
与![]() 的关系为
的关系为![]() ;
;
(2)设![]() ,定义函数
,定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以首项为1,公比为
是以首项为1,公比为![]() 的等比数列,
的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]()
![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数![]() 为
为![]() 上偶函数,当
上偶函数,当![]() 时
时![]() ,又函数
,又函数![]() 图象关于直线
图象关于直线![]() 对称, 当方程
对称, 当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围。
的取值范围。
(本小题满分14分)
已知:函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 为实数).
为实数).
(1)当 时,求
时,求 的解析式;
的解析式;
(2)若 ,试判断
,试判断 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)是否存在 ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当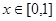 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
查看习题详情和答案>>
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 为实数).
为实数). 时,求
时,求 ,试判断
,试判断 上的单调性,并证明你的结论;
上的单调性,并证明你的结论; ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出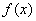 是定义在
是定义在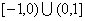 上的偶函数,当
上的偶函数,当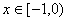 时,
时,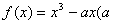 为实数).
为实数).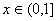 时,求
时,求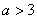 ,试判断
,试判断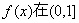 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;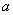 ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出