摘要:17.解:⑴ 当时.. 1分 当时... 2分 是以为首项.以为公比的等比数列. 4分 由于. 5分 是以为首项.以为公差的等差数列. 7分 ⑵ 由⑴知:. 9分 现在只要证明:当时..用数学归纳法证明: (I)当时.有左边=.右边=.不等式成立 10分 (II)假设当时.不等式成立.即. 那么当时.有 当时.恒有成立. 即 当时.不等式也成立 13分 由知.当时. 有. 14分
网址:http://m.1010jiajiao.com/timu3_id_4470820[举报]
定义: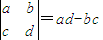 ,设
,设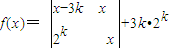 (x∈R,k为正整数)
(x∈R,k为正整数)
(1)分别求出当k=1,k=2时方程f(x)=0的解
(2)设f(x)≤0的解集为[a2k-1,a2k],求a1+a2+a3+a4的值及数列{an}的前2n项和
(3)对于(2)中的数列{an},设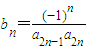 ,求数列{bn}的前n项和Tn的最大值.
,求数列{bn}的前n项和Tn的最大值.
查看习题详情和答案>>
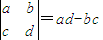 ,设
,设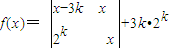 (x∈R,k为正整数)
(x∈R,k为正整数)(1)分别求出当k=1,k=2时方程f(x)=0的解
(2)设f(x)≤0的解集为[a2k-1,a2k],求a1+a2+a3+a4的值及数列{an}的前2n项和
(3)对于(2)中的数列{an},设
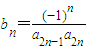 ,求数列{bn}的前n项和Tn的最大值.
,求数列{bn}的前n项和Tn的最大值.查看习题详情和答案>>
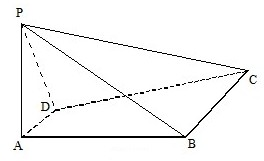 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2| 2 |
(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段GC上运动时,试提出一个研究有关四面P-BMN的问题(如体积、线面、面面关系等)并尝试解决.
(说明:本小题将根据你提出的问题的质量和解决难度分层评分;本小题的计算结果可以使用近似值,保留3位小数) 查看习题详情和答案>>
如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足 ,
, .
.
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过定点F(1,0)作互相垂直的直线l与l',l与(1)中的轨迹C交于A、B两点,l'与(1)中的轨迹C交于D、E两点,求四边形ADBE面积S的最小值;
(3)(在下列两题中,任选一题,写出计算过程,并求出结果,若同时选做两题,
则只批阅第②小题,第①题的解答,不管正确与否,一律视为无效,不予批阅):
①将(1)中的曲线C推广为椭圆: ,并
,并
将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解;
②(解答本题,最多得9分)将(1)中的曲线C推广为椭圆: ,并
,并
将(2)中的定点取为原点,求与(2)相类似的问题的解.
 查看习题详情和答案>>
查看习题详情和答案>>
 ,
, .
.(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过定点F(1,0)作互相垂直的直线l与l',l与(1)中的轨迹C交于A、B两点,l'与(1)中的轨迹C交于D、E两点,求四边形ADBE面积S的最小值;
(3)(在下列两题中,任选一题,写出计算过程,并求出结果,若同时选做两题,
则只批阅第②小题,第①题的解答,不管正确与否,一律视为无效,不予批阅):
①将(1)中的曲线C推广为椭圆:
 ,并
,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解;
②(解答本题,最多得9分)将(1)中的曲线C推广为椭圆:
 ,并
,并将(2)中的定点取为原点,求与(2)相类似的问题的解.
 查看习题详情和答案>>
查看习题详情和答案>>
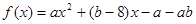 ,当
,当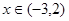 时,
时, 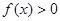 ;
;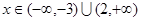 时,
时,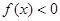
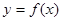 的解析式
的解析式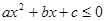 的解集为R.
的解集为R.