摘要：19． 已知点A(7.0)在曲线上.且曲线C在点A处的切线与直线垂直.又当时.函数有最小值. (I)求实数a.b.c的值, (II)设函数的最大值为M. 求正整数的值.使得成立. 20 函数是定义域为R的偶函数.且对任意的.均有成立．当时. (1)当时.求的表达式, (2)若的最大值为.解关于x的不等式．
网址：http://m.1010jiajiao.com/timu3_id_4470787[举报]
本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分.作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。
（1）（本小题满分7分）选修4-2：矩阵与变换
已知向量
=
，变换T的矩阵为A=
，平面上的点P（1，1）在变换T
作用下得到点P′（3，3），求A4.
（2）（本小题满分7分）选修4-4：坐标系与参数方程
直线
与圆
（
>0）相交于A、B两点，设
P（－1，0），且|PA|:|PB|=1:2，求实数的值
（3）（本小题满分7分）选修4-5：不等式选讲
对于x∈R，不等式|x－1|+|x－2|≥
2+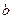
2恒成立，试求2+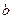的最大值。
（1）（本小题满分7分）选修4-2：矩阵与变换
已知向量
=，变换T的矩阵为A=，平面上的点P（1，1）在变换T作用下得到点P′（3，3），求A4
.（2）（本小题满分7分）选修4-4：坐标系与参数方程
直线
与圆（>0）相交于A、B两点，设P（－1，0），且|PA|:|PB|=1:2，求实数
的值（3）（本小题满分7分）选修4-5：不等式选讲
对于x∈R，不等式|x－1|+|x－2|≥
2+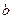2恒成立，试求2+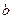的最大值。本题有(1)．(2)．(3)三个选做题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）(本小题满分7分)选修4－2：矩阵与变换选做题
已知矩阵A=
有一个属于特征值1的特征向量
.
(Ⅰ) 求矩阵A；
(Ⅱ) 矩阵B=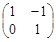
，点O(0,0)，M(2，-1)，N(0，2)，求
在矩阵AB的对应变换作用下所得到的
的面积.
（2）(本小题满分7分)选修4－4：坐标系与参数方程选做题
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系.已知曲线
的参数方程为
，曲线
的极坐标方程为
．
（Ⅰ）将曲线的参数方程化为普通方程；（Ⅱ）判断曲线与曲线的交点个数，并说明理由．
（3）(本小题满分7分)选修4－5：不等式选讲选做题
已知函数
，不等式
在
上恒成立．
（Ⅰ）求
的取值范围；
（Ⅱ）记的最大值为
，若正实数
满足
，求
的最大值．
查看习题详情和答案>>
本小题设有（1）（2）（3）三个选考题，每题7分，请考生任选两题作答，满分14分，如果多做，则按所做的前两题计分．
（1）选修4-2：矩阵与变换
已知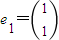
是矩阵
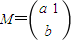属于特征值λ1=2的一个特征向量．
（I）求矩阵M；
（Ⅱ）若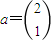
，求M10a．
（2）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，A（l，0），B（2，0）是两个定点，曲线C的参数方程为
为参数）．
（I）将曲线C的参数方程化为普通方程；
（Ⅱ）以A（l，0为极点，|
|为长度单位，射线AB为极轴建立极坐标系，求曲线C的极坐标方程．
（3）选修4-5：不等式选讲
（I）试证明柯西不等式：（a2+b2）（x2+y2）≥（ax+by）2（a，b，x，y∈R）；
（Ⅱ）若x2+y2=2，且|x|≠|y|，求
的最小值．
查看习题详情和答案>>
（1）选修4-2：矩阵与变换
已知
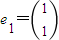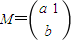是矩阵属于特征值λ1=2的一个特征向量．（I）求矩阵M；
（Ⅱ）若
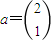，求M10a．（2）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，A（l，0），B（2，0）是两个定点，曲线C的参数方程为
为参数）．（I）将曲线C的参数方程化为普通方程；
（Ⅱ）以A（l，0为极点，|
|为长度单位，射线AB为极轴建立极坐标系，求曲线C的极坐标方程．（3）选修4-5：不等式选讲
（I）试证明柯西不等式：（a2+b2）（x2+y2）≥（ax+by）2（a，b，x，y∈R）；
（Ⅱ）若x2+y2=2，且|x|≠|y|，求
的最小值．查看习题详情和答案>>
本题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分，作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
设矩阵 M=
（其中a＞0，b＞0）．
（Ⅰ）若a=2，b=3，求矩阵M的逆矩阵M-1；
（Ⅱ）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′：
+y2=1，求a，b的值．
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系xOy中，直线l的方程为x-y+4=0，曲线C的参数方程为
(∂为参数)．
（Ⅰ）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
（3）（本小题满分7分）选修4-5：不等式选讲
设不等式|2x-1|＜1的解集为M．
（Ⅰ）求集合M；
（Ⅱ）若a，b∈M，试比较ab+1与a+b的大小． 查看习题详情和答案>>
（1）选修4-2：矩阵与变换
设矩阵 M=
|
（Ⅰ）若a=2，b=3，求矩阵M的逆矩阵M-1；
（Ⅱ）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′：
| x2 |
| 4 |
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系xOy中，直线l的方程为x-y+4=0，曲线C的参数方程为
|
（Ⅰ）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
| π |
| 2 |
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
（3）（本小题满分7分）选修4-5：不等式选讲
设不等式|2x-1|＜1的解集为M．
（Ⅰ）求集合M；
（Ⅱ）若a，b∈M，试比较ab+1与a+b的大小． 查看习题详情和答案>>
本题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分，作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
设矩阵 M=
（其中a＞0，b＞0）．
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’：
+y2=1，求a，b的值．
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系xOy中，直线l的方程为x-y+4=0，曲线C的参数方程为
(∂为参数)．
（I）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
（II）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
（3）（本小题满分7分）选修4-5：不等式选讲
设不等式|2x-1|＜1的解集为M．
（I）求集合M；
（II）若a，b∈M，试比较ab+1与a+b的大小．
查看习题详情和答案>>
（1）选修4-2：矩阵与变换
设矩阵 M=
|
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’：
| x2 |
| 4 |
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系xOy中，直线l的方程为x-y+4=0，曲线C的参数方程为
|
（I）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
| π |
| 2 |
（II）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
（3）（本小题满分7分）选修4-5：不等式选讲
设不等式|2x-1|＜1的解集为M．
（I）求集合M；
（II）若a，b∈M，试比较ab+1与a+b的大小．