��Ŀ����
�������У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ʒ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������У�
��1��ѡ��4-2��������任
����� M=
������a��0��b��0����
��I����a=2��b=3�������M�������M-1��
��II��������C��x2+y2=1�ھ���M����Ӧ�����Ա任�����µõ�����C����
+y2=1����a��b��ֵ��
��2������С������7�֣�ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�ֱ��l�ķ���Ϊx-y+4=0������C�IJ�������Ϊ
(∂Ϊ����)��
��I����֪�ڼ����꣨��ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У���P�ļ�����Ϊ��4��
�����жϵ�P��ֱ��l��λ�ù�ϵ��
��II�����Q������C�ϵ�һ�����㣬������ֱ��l�ľ������Сֵ��
��3������С������7�֣�ѡ��4-5������ʽѡ��
�費��ʽ|2x-1|��1�Ľ⼯ΪM��
��I����M��
��II����a��b��M���ԱȽ�ab+1��a+b�Ĵ�С��
��1��ѡ��4-2��������任
����� M=
|
��I����a=2��b=3�������M�������M-1��
��II��������C��x2+y2=1�ھ���M����Ӧ�����Ա任�����µõ�����C����
| x2 |
| 4 |
��2������С������7�֣�ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�ֱ��l�ķ���Ϊx-y+4=0������C�IJ�������Ϊ
|
��I����֪�ڼ����꣨��ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У���P�ļ�����Ϊ��4��
| �� |
| 2 |
��II�����Q������C�ϵ�һ�����㣬������ֱ��l�ľ������Сֵ��
��3������С������7�֣�ѡ��4-5������ʽѡ��
�費��ʽ|2x-1|��1�Ľ⼯ΪM��
��I����M��
��II����a��b��M���ԱȽ�ab+1��a+b�Ĵ�С��
��1����I����M=
��M-1=
��a=2��b=3���뼴�ã�M-1=
=
��II���������C��x2+y2=1����һ��Ϊ��x0��y0��������M����Ӧ�����Ա任�����µõ��ĵ�Ϊ��x��y����
��M��x0��y0��=��x��y��
��
��֮����
+y2=1�ã�
+b2
=1
��
��a��0��b��0
��
��2����I�����P�ļ�����Ϊ��4��
����
��P��ֱ������Ϊ��0��4��
��ֱ��l�ķ���Ϊx-y+4=0
�ࣨ0��4����ֱ��l��
��II��������C�IJ�������Ϊ
(∂Ϊ����)��ֱ��l�ķ���Ϊx-y+4=0
������C�ĵ�ֱ��l�ľ���Ϊd
��d=
=
��2sin��
-������[-2��2]
��d����СֵΪ
��3����I����|2x-1|��1
��-1��2x-1��1
��0��x��1
��MΪ{x|0��x��1}
��II��a��b��M
��a-1��0��b-1��0
�ࣨb-1����a-1����0
�ࣨab+1��-��a+b��=a��b-1��+��1-b��=��b-1����a-1����0
����ab+1������a+b��
|
��M-1=
|
��a=2��b=3���뼴�ã�M-1=
|
|
��II���������C��x2+y2=1����һ��Ϊ��x0��y0��������M����Ӧ�����Ա任�����µõ��ĵ�Ϊ��x��y����
��M��x0��y0��=��x��y��
��
|
��֮����
| x2 |
| 4 |
a2
| ||
| 4 |
| y | 20 |
��
|
��a��0��b��0
��
|
��2����I�����P�ļ�����Ϊ��4��
| �� |
| 2 |
|
��P��ֱ������Ϊ��0��4��
��ֱ��l�ķ���Ϊx-y+4=0
�ࣨ0��4����ֱ��l��
��II��������C�IJ�������Ϊ
|
������C�ĵ�ֱ��l�ľ���Ϊd
��d=
|
| ||
|
|4+2sin(
| ||
|
��2sin��
| �� |
| 3 |
��d����СֵΪ
| 2 |
��3����I����|2x-1|��1
��-1��2x-1��1
��0��x��1
��MΪ{x|0��x��1}
��II��a��b��M
��a-1��0��b-1��0
�ࣨb-1����a-1����0
�ࣨab+1��-��a+b��=a��b-1��+��1-b��=��b-1����a-1����0
����ab+1������a+b��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 �ǽ�ƽ����ÿ����
�ǽ�ƽ����ÿ���� �ĺ������
������ ���������
��������� ���䵽��
���䵽�� .
. �ڱ任
�ڱ任 �ļ����귽��Ϊ��
�ļ����귽��Ϊ�� ��ֱ��
��ֱ�� �IJ�������Ϊ��
�IJ��������� ��
�� ������.
������. ������
������ ��ֵ��
��ֵ�� Ϊʵ������
Ϊʵ������

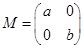 ������a��0��b��0��.
������a��0��b��0��.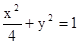 ����a��b��ֵ.
����a��b��ֵ. ������a��0��b��0����
������a��0��b��0����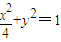 ����a��b��ֵ��
����a��b��ֵ�� ��
�� �����жϵ�P��ֱ��l��λ�ù�ϵ��
�����жϵ�P��ֱ��l��λ�ù�ϵ��