摘要： 如图所示.四边形ABCD是某个圆的圆外切四边形.已知∠A＝∠B＝120°.∠D＝90°,且BC＝1.则AD的长为
网址：http://m.1010jiajiao.com/timu3_id_4470341[举报]
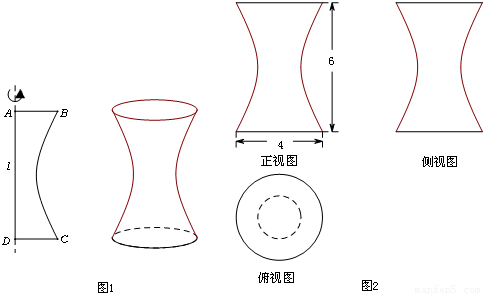
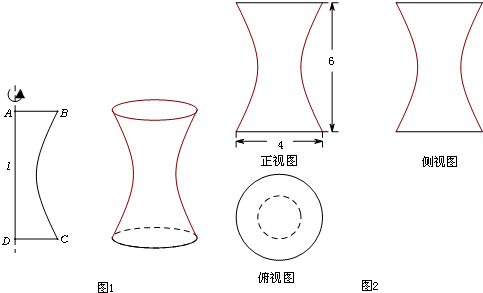
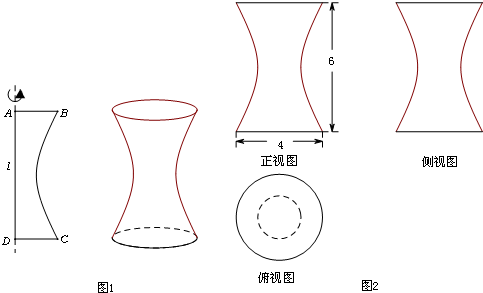
如图1所示，一平面曲边四边形ABCD中，曲边BC是某双曲线的一部分，该双曲线的虚轴所在直线为l，边AD在直线l上，四边形ABCD绕直线l旋转得到一个几何体．若该几何体的三视图及其部分尺寸如图2所示，其中俯视图中小圆的半径为1，则该双曲线的离心率是（ ）
A．3
B．4
C．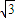
D．2
查看习题详情和答案>>
A．3
B．4
C．
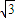
D．2
查看习题详情和答案>>
如图1所示，一平面曲边四边形ABCD中，曲边BC是某双曲线的一部分，该双曲线的虚轴所在直线为l，边AD在直线l上，四边形ABCD绕直线l旋转得到一个几何体．若该几何体的三视图及其部分尺寸如图2所示，其中俯视图中小圆的半径为1，则该双曲线的离心率是
- A.3
- B.4
- C.
- D.2
（2012•泉州模拟）如图1所示，一平面曲边四边形ABCD中，曲边BC是某双曲线的一部分，该双曲线的虚轴所在直线为l，边AD在直线l上，四边形ABCD绕直线l旋转得到一个几何体．若该几何体的三视图及其部分尺寸如图2所示，其中俯视图中小圆的半径为1，则该双曲线的离心率是（ ）
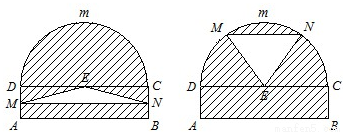
（本小题满分16分）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是等腰梯形，其中高0.5米，AB=1米， CD=2a（a＞
）米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆．
（1）设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S（平方米）表示成关于x的函数
；
（2）当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．
）米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆．（1）设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S（平方米）表示成关于x的函数
；（2）当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．
某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=0.5米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆（MN和AB、DC不重合）．
（1）当MN和AB之间的距离为1米时，求此时三角通风窗EMN的通风面积；
（2）设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S（平方米）表示成关于x的函数S=f（x）；
（3）当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．
查看习题详情和答案>>
（1）当MN和AB之间的距离为1米时，求此时三角通风窗EMN的通风面积；
（2）设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S（平方米）表示成关于x的函数S=f（x）；
（3）当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．
查看习题详情和答案>>