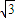题目内容
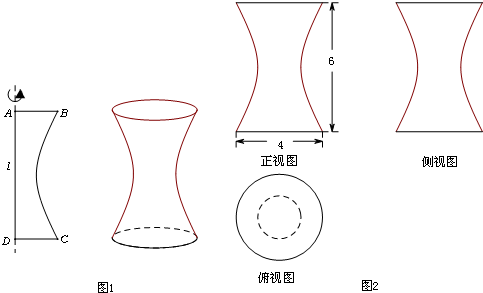
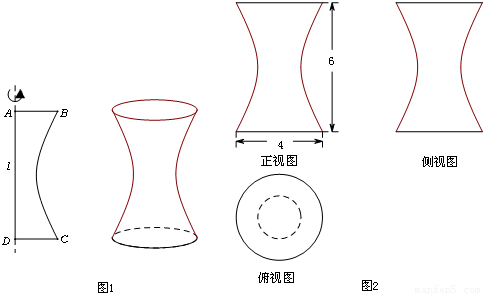
如图1所示,一平面曲边四边形ABCD中,曲边BC是某双曲线的一部分,该双曲线的虚轴所在直线为l,边AD在直线l上,四边形ABCD绕直线l旋转得到一个几何体.若该几何体的三视图及其部分尺寸如图2所示,其中俯视图中小圆的半径为1,则该双曲线的离心率是
- A.3
- B.4
- C.

- D.2
D
分析:设双曲线方程,根据三视图可得a=1,(2,3)在双曲线上,代入双曲线方程,即可求得双曲线的离心率.
解答:由题意,可设双曲线方程为 ,则
,则
根据三视图可得a=1,(2,3)在双曲线上,代入双曲线方程可得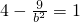
∴b2=3,∴c2=a2+b2=4
∴c=2
∴双曲线的离心率是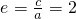
故选D.
点评:本题考查三视图,考查双曲线的几何性质,正确确定双曲线的方程是关键.
分析:设双曲线方程,根据三视图可得a=1,(2,3)在双曲线上,代入双曲线方程,即可求得双曲线的离心率.
解答:由题意,可设双曲线方程为
 ,则
,则根据三视图可得a=1,(2,3)在双曲线上,代入双曲线方程可得
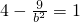
∴b2=3,∴c2=a2+b2=4
∴c=2
∴双曲线的离心率是
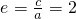
故选D.
点评:本题考查三视图,考查双曲线的几何性质,正确确定双曲线的方程是关键.

练习册系列答案
相关题目