摘要：20．设A(x1,y1),B(x2,y2)是函数f(x)=的图象上任意两点.且.已知点M的横坐标为. (1) 求证:M点的纵坐标为定值, (2) 若Sn=f(∈N*.且n≥2,求Sn; (3) 已知an=.其中n∈N*. Tn为数列{an}的前n项和.若Tn＜λ(Sn+1+1)对一切n∈N*都成立.试求λ的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_4470271[举报]
已知A(x1,y1),B(x2,y2)是函数f(x)=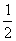
的图象上的任意两点(可以重合),点M在直线x=
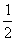上,且
=
.
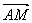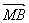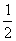的图象上的任意两点(可以重合),点M在直线x=上,且=.(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f(
)+f(
)+f(
)+…+f(
),求Sn;
(3)在(2)的条件下,设an=2Sn,Tn为数列{an}的前n项和,若存在正整数c、m,使得不等式
＜
成立,求c和m的值.
已知A(x1,y1),B(x2,y2)是函数f(x)=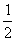
的图象上的任意两点(可以重合),点M在直线x=
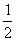上,且
=
.
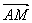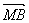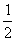的图象上的任意两点(可以重合),点M在直线x=上,且=.(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f(
)+f(
)+f(
)+…+f(
),求Sn;
(3)在(2)的条件下,设an=
,Tn为数列{an}的前n项和,若存在正整数c、m,使得不等式
成立,求c和m的值.
设函数f(x)=
，g(x)=lnx．
（1）试判断当x＞0，g（x）与f（x）的大小关系；
（2）求证：（1+1•2）（1+2•3）…[1+n（n+1）]＞e2n-3（n∈N*）；
（3）设A（x1，y1）、B（x2，y2）（x1＜x2）是函数y=g（x）的图象上的两点，且g′（x0）=
（其中g′（x）为g（x）的导函数），证明：x0∈（x1，x2）．
查看习题详情和答案>>
| 2x-3 |
| x |
（1）试判断当x＞0，g（x）与f（x）的大小关系；
（2）求证：（1+1•2）（1+2•3）…[1+n（n+1）]＞e2n-3（n∈N*）；
（3）设A（x1，y1）、B（x2，y2）（x1＜x2）是函数y=g（x）的图象上的两点，且g′（x0）=
| y1-y2 |
| x2-x1 |