摘要： 已知数列{an}满足:a1＝.且an＝ (1) 求数列{an}的通项公式, (2) 证明:对于一切正整数n.不等式a1·a2·--an<2·n! 普通高等学校招生全国统一考试 理科数学 本试卷分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷1至2页.第Ⅱ卷3至4页.全卷满分150分.考试时间120分钟. 参考公式: 如果时间A.B互斥.那么 如果时间A.B相互独立.那么 如果事件A在一次试验中发生的概率是P.那么n次独立重复试验中恰好发生k次的概率 球的表面积公式.其中R表示球的半径 球的体积公式.其中R表示球的半径 第Ⅰ卷
网址：http://m.1010jiajiao.com/timu3_id_4468950[举报]
（本小题满分14分）已知f(x)=ln(1+x)-x.
（Ⅰ）求f(x)的最大值；
（Ⅱ）数列{an}满足：an+1= 2f' (an) +2,且a1=2.5，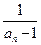
= bn,
⑴数列{ bn+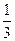
}是等比数列 ⑵判断{an}是否为无穷数列。
（Ⅲ）对n∈N*,用⑴结论证明：ln(1+
+
)<;
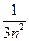（本小题满分14分）已知f(x)=ln(1+x)-x.
（Ⅰ）求f(x)的最大值；
（Ⅱ）数列{an}满足：an+1= 2f' (an) +2,且a1=2.5，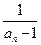
= bn,
⑴数列{ bn+
}是等比数列 ⑵判断{an}是否为无穷数列。
（Ⅲ）对n∈N*,用⑴结论证明：ln(1+
+
)<;
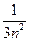（Ⅰ）求f(x)的最大值；
（Ⅱ）数列{an}满足：an+1= 2f' (an) +2,且a1=2.5，
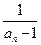= bn,⑴数列{ bn+
}是等比数列 ⑵判断{an}是否为无穷数列。（Ⅲ）对n∈N*,用⑴结论证明：ln(1+
+)<; 
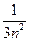，求数列{bn}的前n项和S
，求数列{bn}的前n项和S