摘要: 已知函数, 数列{}满足: 证明: (I).; (II).. 证明: (I).先用数学归纳法证明.n=1,2,3,- (i).当n=1时,由已知显然结论成立. (ii).假设当n=k时结论成立,即.因为0<x<1时 ,所以f上是增函数. 又f(x)在[0,1]上连续, 从而.故n=k+1时,结论成立. 由可知.对一切正整数都成立. 又因为时.. 所以.综上所述. (II).设函数..由(I)知.当时.. 从而 所以g 上是增函数. 又g (x)在[0,1]上连续,且g (0)=0, 所以当时.g (x)>0成立.于是. 故.
网址:http://m.1010jiajiao.com/timu3_id_4468922[举报]
(本小题满分14分)已知函数![]() 满足:
满足:![]() ;(1)分别写出
;(1)分别写出![]() 时
时![]() 的解析式
的解析式![]() 和
和![]() 时
时![]() 的解析式
的解析式![]() ;并猜想
;并猜想![]() 时
时![]() 的解析式
的解析式![]() (用
(用![]() 和
和![]() 表示)(不必证明)(2分)(2)当
表示)(不必证明)(2分)(2)当![]()
![]() 时,
时,![]()
![]() 的图象上有点列
的图象上有点列![]() 和点列
和点列![]() ,线段
,线段![]() 与线段
与线段![]() 的交点
的交点![]() ,求点
,求点![]() 的坐标
的坐标![]() ;(4分)
;(4分)
(3)在前面(1)(2)的基础上,请你提出一个点列![]() 的问题,并进行研究,并写下你研究的过程 (8分)
的问题,并进行研究,并写下你研究的过程 (8分)
 .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列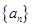 满足
满足 ,求
,求 时,求证:
时,求证: .
.